2015-05-10
330
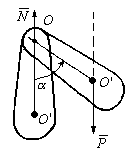
Рис. 2
|
Тело, совершающее колебания около неподвижной оси, не проходящей через его центр масс, называется физическим маятником. В данном случае тело совершает возвратно-вращательное движение. На рис.2 О след оси вращения на плоскости чертежа; ОО ¢=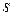 
– расстояние от оси вращения до центра масс маятника. К телу приложены силы: тяжести 
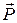и реакции оси 
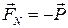. Момент относительно оси вращения создает только сила 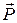. Уравнение движения маятника запишется в виде:
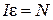, (6)
где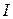 
– момент инерции тела относительно оси колебания; 
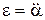– угловое ускорение тела; 
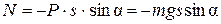, знак «–» имеет то же объяснение, что и в случае математического маятника. После соответствующих подстановок приходим к уравнению движения в виде:
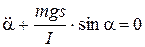. (7)
Для случая малых колебаний уравнение запишется в виде
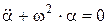, (8)
где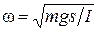 
. Решением данного дифференциального уравнения будет функция
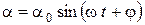. (9)
Амплитуда колебаний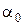 
и начальная фаза определяются начальными условиями, а вот частота и период колебаний Т определяются параметрами физического маятника
; 
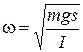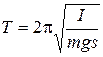. (10)
Здесь мы снова видим, что колебания маятника изохронны, таким образом, в принципе эти формулы можно использовать для определения ускорения силы тяжести.
