Задан закон распределения  случайной величины
случайной величины 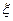 (приложение 1). Требуется:
(приложение 1). Требуется:
a) Для каждого из 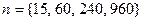 , сгенерировать, используя генератор случайных чисел пакета EXCEL, по 10 выборок объемом
, сгенерировать, используя генератор случайных чисел пакета EXCEL, по 10 выборок объемом 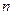 из генеральной совокупности
из генеральной совокупности  (для генерации случайных чисел распределенных по законам, которые отсутствуют в генераторе случайных чисел пакета EXCEL см. приложение 2). Для каждой выборки определить среднее:
(для генерации случайных чисел распределенных по законам, которые отсутствуют в генераторе случайных чисел пакета EXCEL см. приложение 2). Для каждой выборки определить среднее: 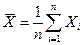 , данные представить в виде таблицы:
, данные представить в виде таблицы:
Выборочное среднее 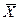
| ||||
| N п/п выборки | n=15 | n=60 | n=240 | n=960 |
| … | ||||
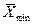
| ||||
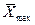
| ||||
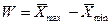
|
Таблица 1. Значения выборочных средних 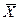 для выборок различного объема
для выборок различного объема
Оценить изменение величины разброса 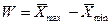 с ростом объема выборки. Сделать выводы о сходимости выборочных характеристик.
с ростом объема выборки. Сделать выводы о сходимости выборочных характеристик.
b) Если наблюдается сходимость выборочного среднего, используя центральную предельную теорему определить для заданной в задании (приложение 1) вероятности 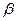 и величины отклонения
и величины отклонения 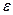 необходимый объем выборки N, так чтобы
необходимый объем выборки N, так чтобы 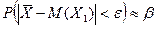 . Проверить, сгенерировав 10 выборок найденного объема
. Проверить, сгенерировав 10 выборок найденного объема 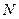 и подсчитав для каждой величину
и подсчитав для каждой величину 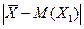 .
.
|
|
|
Примечание. Указанные в задании действия проделать для каждого из двух законов распределений, указанных в варианте задания.
Приложение 1. Варианты заданий.
Вариант 1.
1)  - закон равномерной плотности на (1; 3).
- закон равномерной плотности на (1; 3). 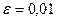 ,
, 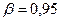 .
.
2)  - закон с плотностью распределения
- закон с плотностью распределения 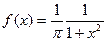 ,
, 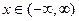 .
. 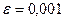 ,
, 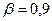 .
.
Вариант 2.
1)  - нормальный закон с параметрами
- нормальный закон с параметрами 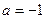 и
и 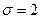 .
. 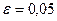 ,
, 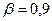 .
.
2)  - закон с плотностью распределения
- закон с плотностью распределения 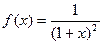 ,
, 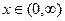 .
. 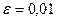 ,
, 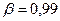 .
.
Вариант 3.
1)  - биномиальное распределение с
- биномиальное распределение с 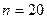 и
и 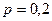 .
. 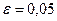 ,
, 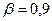 9.
9.
2)  - закон с плотностью распределения
- закон с плотностью распределения 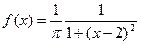 ,
, 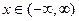 .
. 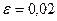 ,
, 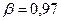 .
.
Вариант 4.
1).  - закон Пуассона с параметром
- закон Пуассона с параметром 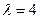 .
. 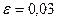 ,
, 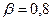 .
.
2).  - закон с плотностью распределения
- закон с плотностью распределения 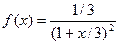 ,
, 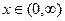 .
. 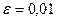 ,
, 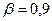 .
.
Вариант 5.
1.  - показательный закон с параметром
- показательный закон с параметром 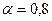 .
. 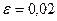 ,
, 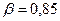 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 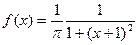 ,
, 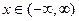 .
. 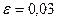 ,
, 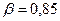
Вариант 6.
1.  - показательный закон с параметром.
- показательный закон с параметром. 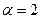 .
. 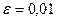 ,
, 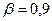 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 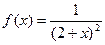 ,
, 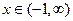 .
. 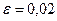 ,
, 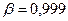 .
.
Вариант 7.
1.  - закон Бернулли с параметром
- закон Бернулли с параметром 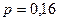 .
. 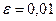 ,
, 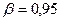 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 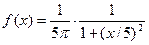 ,
, 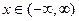 .
. 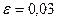 ,
, 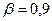 .
.
Вариант 8.
1.  - нормальный закон с параметрами
- нормальный закон с параметрами 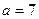 и
и 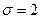 .
. 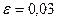 ,
, 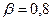 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 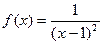 ,
, 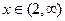 .
. 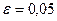 ,
, 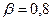 .
.
Вариант 9.
1.  - биномиальный закон с параметрами
- биномиальный закон с параметрами 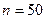 и
и 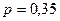 .
. 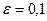 ,
, 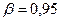 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 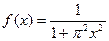 ,
, 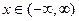 .
. 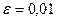 ,
, 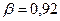 .
.
Вариант 10.
1.  - закон равномерной плотности на (-3; 3).
- закон равномерной плотности на (-3; 3). 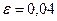 ,
, 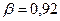 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 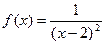 ,
, 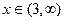 .
. 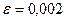 ,
, 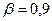 .
.
Вариант 11.
1.  - нормальный закон с параметрами
- нормальный закон с параметрами 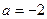 и
и 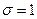 .
. 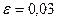 ,
, 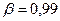 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 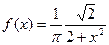 ,
, 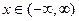 .
. 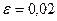 ,
, 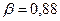 .
.
Вариант 12.
1.  - биномиальное распределение с
- биномиальное распределение с 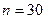 и
и 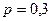 .
. 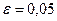 ,
, 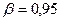 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 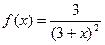 ,
, 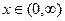 .
. 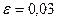 ,
,  .
.
Вариант 13.
1.  - закон Пуассона с параметром
- закон Пуассона с параметром 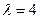 .
. 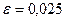 ,
, 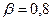 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 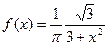 ,
, 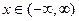 .
. 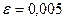 ,
, 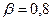 .
.
Вариант 14.
|
|
|
1.  - показательный закон с параметром
- показательный закон с параметром 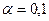 .
. 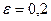 ,
, 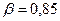 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 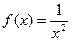 ,
, 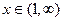 .
. 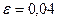 ,
, 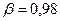 .
.
Вариант 15.
1.  - нормальный закон с параметрами
- нормальный закон с параметрами 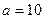 и
и 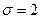 .
. 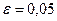 ,
, 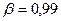 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 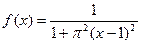 ,
, 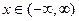 .
. 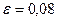 ,
, 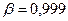 .
.
Вариант 16.
1.  - закон Бернулли с параметром
- закон Бернулли с параметром 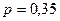 .
. 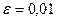 ,
, 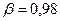 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 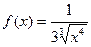 ,
, 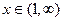 .
. 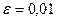 ,
, 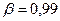 .
.
Вариант 17.
1.  - нормальный закон с параметрами
- нормальный закон с параметрами 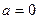 и
и 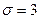 .
. 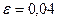 ,
, 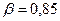 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 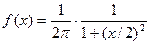 ,
, 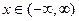 .
. 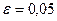 ,
, 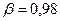 .
.
Вариант 18.
1.  - биномиальный закон с параметрами
- биномиальный закон с параметрами 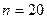 и
и 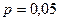 .,
., 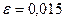 ,
, 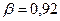 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 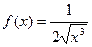 ,
, 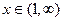 .
. 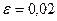 ,
, 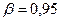 .
.
Вариант 19.
1.  - закон равномерной плотности на
- закон равномерной плотности на 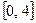 .
. 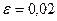 ,
, 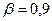 .
.
2.  - закон с плотностью распределения
- закон с плотностью распределения 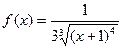 ,
, 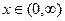 .
. 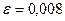 ,
, 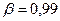 .
.
Вариант 20.
3.  - показательный закон с параметром
- показательный закон с параметром 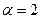 .
. 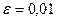 ,
, 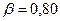 .
.
4.  - закон с плотностью распределения
- закон с плотностью распределения 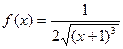 ,
, 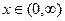 .
. 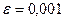 ,
, 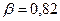 .
.
Приложение 2. Генерация случайных чисел.
 2015-05-10
2015-05-10 384
384








