Лабораторная работа № 3
Условный оператор
Цель работы: приобрести навыки в решении задач с помощью условного оператора, усвоить назначение и правила его применения.
Основы теории
1. Условный оператор if
Очень часто на практике ход решение задачи зависит от выполнения какого-либо условия. В этом случае при программировании необходимо использовать условный оператор (рисунки 1, 2).
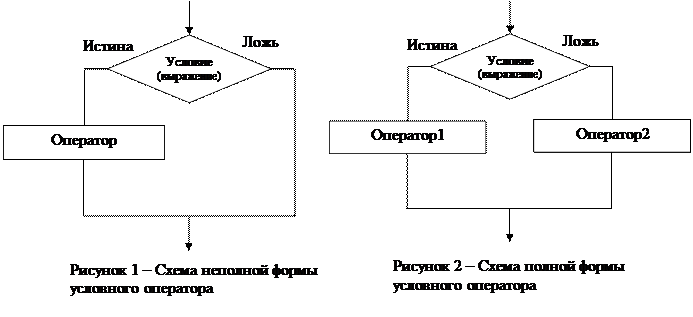
В языке С существуют три возможных варианта организации ветвлений (таблица 1).
Таблица 1
| Формат условного оператора | Форма | Комментарий |
| If (Выражение)Оператор; | неполная форма условного оператора | Если Выражение истинно, то выполняется Оператор, если выражение ложно, то выполняется следующий за if оператор |
| if(Выражение)Оператор1; еlse Оператор2; | полная форма условного оператора | Если Выражение истинно, то выполняется Оператор1, если ложно – Оператор2 |
| Switch | Оператор выбора | Реализуется многоальтернативное ветвление |
Выполнение оператора if начинается с вычисления выражения. Выражение в записи формата условного оператора – это некоторое условие, содержащее операции отношения и логические операции.
Операции отношения – это операции, перечисленные в таблице 2. Результатом операции отношения является целое число (0 – ложь или 1 – истина).
Таблица 2– Операции отношения
| Обозначение | Значение |
| > | Больше |
| >= | больше или равно |
| < | Меньше |
| <= | меньше или равно |
| = = | равно (сравнение на равенство) |
| != | не равно |
Логические операции – это операции, перечисленные в таблице 3.
Таблица 3 – Логические операции
| Битовые логические операции | Логические операции | ||
| & | and, и | && | and, и |
| | | or, или | || | or, или |
| ~ | отрицание not, не | ! | отрицание not, не |
| ^ | исключающее или, xor |
Выражения (a==1) && (b>2) и (a== 1) & (b>2) с точки зрения компилятора С являются синтаксически правильными, т.к. в результате выполнения операций отношения = = и > получаются целые числа, с которыми можно производить как логическую операцию &&, так и битовую операцию &.
Таблица 4 – Таблицы истинности для логических операций
| X | Y | X and Y | X | Y | X or Y | X | not X | |||||
 2015-05-10
2015-05-10 324
324








