Задача № 2. Дана интегральная функция F(x) распределения непрерывной случайной величины

Дана интегральная функция F(x) распределения непрерывной случайной величины: .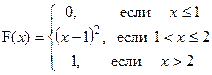

Требуется: 1) убедиться, что заданная функция F(x) является функцией распределения, проверив свойства функции; 2) найти плотность данного распределения f(x); 3) построить графики интегральной и дифференциальной функций распределения.

Решение. 1) На левом конце участка 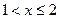заданной функции имеем: F(1)= 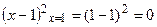, а на правом конце участка: F(2)= 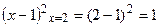. Так как выполняется свойство непрерывности функции распределения, то F(x) является интегральной функцией распределения непрерывной случайной величины.

2) Плотность распределения или дифференциальная функция распределения непрерывной случайной величины находится по формуле: 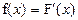, т.е. в данном случае:

.

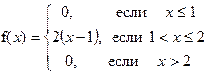3)

Рис.1