2015-05-10
1505
Случайная величина Х распределена по нормальному закону. Известно её математическое ожидание а и среднее квадратическое отклонение s. 1)Найти вероятность того, что Х примет значение, принадлежащее интервалу (a, b). 2) Найти вероятность того, что абсолютная величина отклонения Х - а окажется меньше d. Конкретные значения параметров заданы в таблице.
| Номер задачи | а | s | a | b | d |
Задачи № 11-20
Закон распределения дискретной случайной величины Х задан в таблице. Найти: 1)математическое ожидание, дисперсию и среднее квадратическое отклонение; 2) вычислить математическое ожидание и дисперсию случайной величины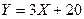 
, пользуясь свойствами математического ожидания и дисперсии.
| Номер задачи | Условие задачи | |||||
| xi | ||||||
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | |
| xi | ||||||
| pi | 0,3 | 0,2 | 0,2 | 0,1 | 0,2 | |
| xi | ||||||
| pi | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 | |
| xi | ||||||
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | |
| xi | ||||||
| pi | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 | |
| xi | ||||||
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | |
| xi | ||||||
| pi | 0,3 | 0,2 | 0,2 | 0,1 | 0,2 | |
| xi | ||||||
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | |
| xi | ||||||
| pi | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 | |
| xi | ||||||
| pi | 0,3 | 0,2 | 0,2 | 0,1 | 0,2 |
