2014-02-02
34363
Определение 25.2. Эмпирической функцией распределения (функцией распределения выборки) называют функцию 
, определяющую для каждого значения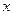 
относительную частоту события 
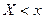, т.е.
,
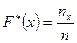где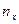 
– число 
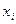, меньших ; 
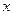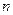– объем выборки.
Из теоремы Бернулли следует, что при достаточно большом объеме выборки функции и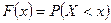 
мало отличаются друг от друга. Отличие эмпирической функции распределения от теоретической состоит в том, что теоретическая функция распределения определяет вероятность события 
, а эмпирическая функция определяет относительную частоту этого же события.
Эмпирическая функция распределения обладает всеми свойствами интегральной функции распределения:
1) значения эмпирической функции распределения принадлежат отрезку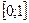 
;
2) – неубывающая функция;
3) если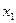 
– наименьшая варианта, то 
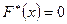при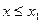 
; если 
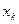– наибольшая варианта, то 
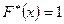при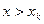 
.
Пример 25.1. Построить эмпирическую функцию по данному распределению выборки:
| Варианты |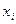
2 | 6 | 10 |
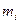 – частоты |
12 | 18 | 30 |
Решение. Найдем объем выборки: 12+18+30=60.
|
|
|
Наименьшая варианта равна 2, следовательно 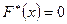при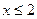 
.
Значение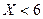 
, а именно 
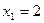, наблюдалось 12 раз, следовательно, 
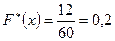при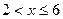 
.
Значения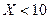 
, а именно 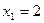и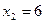 
, наблюдались 12+18=30 раз, следовательно, 
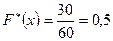при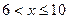 
.
Так как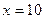 
– наибольшая варианта, то 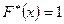при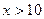 
.
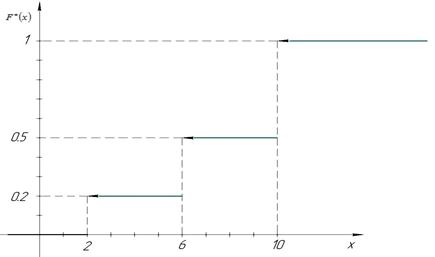
Искомая эмпирическая функция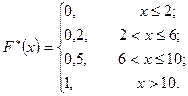 
График этой функции имеет вид:
