В некоторых случаях может оказаться более удобным принцип, основанный на произвольном пороге h. Для этого сформулируем и докажем следующую Теорему.
Теорема 2. Если максимальное число людей, имеющих ключи равно n (здесь уже n - любое целое положительное число) и требуется обеспечить решение при пороге h, то количество фрагментов равно числу кодовых комбинаций в R(n, n-h+1).
k = P(h-1, n-h+1) = 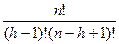 , (5)
, (5)
Пример 2. Пусть n = 6, h = 2. Построим равновесный двоичный код R(6,5)
Таблица 2.
1 2 3 4 5 6
-------------------
1) 1 1 1 1 1 0
2) 1 1 1 1 0 1
3) 1 1 1 0 1 1
4) 1 1 0 1 1 1
5) 1 0 1 1 1 1
6) 0 1 1 1 1 1
Дизъюнкция любых двух столбцов дает код, содержащий все единицы.
Доказательство необходимости и достаточности приведено ниже.
Теорема 2 является обобщением Теоремы 1. Действительно, если положить в Теореме 2 значение h = (n +1)/2, то получим R(n,(n +1)/2).
Обе теоремы являются конструктивными, так как дают правило распределения ключей между членами принимающей команды.
Доказательство. Возьмем i -й столбец из R(n,h) и обозначим его r (i). Его вес будем определять как число единиц в коде и обозначать ½r(i)½ Определим операцию дизъюнкции столбцов r(i) и r(j) в виде результирующего вектора той же размерности, все компоненты которого получены путем дизъюнкции соответствующих компонентов векторов r(i) и r(j). Аналогично введем операцию дизъюнкции "v" над s векторами: r(i1) v r(i2) v r(i3) v...v r(is).
Возьмем полную таблицу кодов длины n веса q, которую мы обозначали R(n,q). Из этой таблицы выберем произвольный столбец с номером i, т.е. r(i). Определим его вес. Легко видеть, что при любом i.
½r(i)½ = P(n-q,q-1) = C 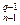 , (4)
, (4)
Вес кода дизъюнкции любых 2 -х столбцов с номерами i и j равен
½r(i) v r(j) ½ = C 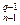 + C
+ C 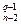
Вес кода дизъюнкции любых s столбцов с номерами i1,i2,i3,...is при
1 < s < n-q+1 равен
½r(i1) v r(i2) v r(i3) v...v r(is)½ = C 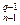 + C
+ C 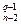 + C
+ C 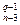 + …+C
+ …+C 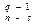 , (6)
, (6)
Если s = n-q+1, то сумма (5) точно равна количеству кодов в R(n,q),
т.е.
C 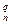 =
= 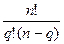
Действительно, последний член в (6) равен 1.
Если число членов s ряда (6) меньше n-q+1, то сумма (6) меньше значения (3), что доказывает теорему, так как никакие члены команды, если их меньше, чем n-q+1 не имеют полного набора ключей. В частном случае, если
q = (n+1)/2, имеем, что при s = (n+1)/2 в совокупности имеется полный набор ключей для расшифровки сообщения.
Приведенный алгоритм распределения фрагментов общего секретного ключа достаточно прост и позволяет найти распределения секрета при любых значениях n и любых h (1 £ h £ n). Это является достоинством приведенного алгоритма. Этот алгоритм имеет существенный недостаток, если общий ключ просто разделять на отдельные участки: чем больше соберется сотрудников (хотя их может быть и меньше h), тем легче им будет подобрать значения недостающих фрагментов. Например, если общий ключ представлял собой 20 разрядное десятичное число и его разделить на фрагменты по 2 разряда, то когда соберутся любые 2 сотрудника, им достаточно будет подобрать значения двух недостающих разрядов, т.е. проверить всего 102 вариантов.
Секретность приведенного алгоритма можно существенно усилить, если формировать фрагменты также как формировались фрагменты в первом примере (при h = n).
Пример 3. Пусть секретный ключ S (S1,S2,S3) имеет вид S = (23,8,11), т.е. представляет собой совокупность трех элементов, где каждый элемент – произвольное положительное целое меньшее некоторого простого числа p.
Девять из десяти фрагментов получим с помощью генератора случайных чисел, при этом совершенно необязательно, чтобы элементы находились в пределах 0 – p-1. Например,
1) (5,32,18)
2) (0,19,3)
3) (36,7,16)
4) (9,11,35)
5) (16,1,28)
6) (25,39,46)
7) (3,0,21)
8) (15,14,2)
9) (35,20,20)
А десятый фрагмент (a10,b10,c10) получим по следующему правилу:
a10 = S1 – a1 – a2 - … - a9 mod p
b10 = S2 – b1 – b2 - … - b9 mod p
c10 = S3 – c1 – c2 - … - с9 mod p
Для рассматриваемого примера получаем:
10) (24,10,25)
Если соберутся вместе любые три или больше сотрудников, то ключ S легко восстанавливается сложением соответствующих элементов всех десяти фрагментов по модулю 29. Если соберется вместе менее трех сотрудников, то на подбор ключа S им потребуется столько же усилий, сколько требуется любому одному сотруднику.
В общем случае при заданных n и h число фрагментов ключей равно
P(h-1,n-h + 1) = n!/((h-1)!(n-h+1)!)
Криптостойкость ключа не зависит от числа сотрудников, если их меньше h и ключ легко собирается, если число сотрудников равно или больше h.
Приведенный метод позволяет производить разделение секрета при различных степенях доверия к сотрудникам. Так, если разделяющий секрет доверяет какому-то лицу больше, чем остальным, он может выделить ему две или даже три “квоты” ключа. Порог, как и ранее можно выбирать любой (но не менее, чем число “квот”, выданных наиболее доверенному сотруднику). Естественно, число сотрудников в такой схеме соответственно уменьшается.
 2015-05-10
2015-05-10 272
272








