2015-05-10
440
8. Вернитесь обратно в тот лист, где размещены исходные данные.
9. Выделите пустую клетку, в которой вы хотите разместить коэффициент корреляции.
10. В главном меню выберите Вставка/функция.
11. В окне Категория выберите Статистические, затем в окне Функция – КОРРЕЛ. Заполните диалоговое окно. Щелкните по кнопке ОК.
12. Сделайте вывод.
Выполните четвертый пункт. Оцените статистическую значимость параметров регрессии, используя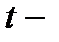 
статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей с 95% надежностью.
Воспользуемся статистикой Стьюдента. По условию уровень надежности 95%, значит, уровень значимости равен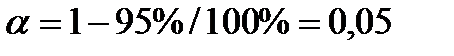 
.
13. Оцените значимость коэффициентов регрессии с помощью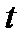 
– статистики Стьюдента.
1) Выдвигаем нулевую гипотезу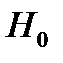 
об отсутствии линейной связи между переменным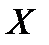и 
и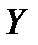 
. Конкурирующая гипотеза 
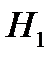– между переменным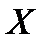и 
и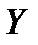 
существует линейная связь.
2) Из столбца «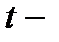
статистика» таблицы 3 находим 
, 
.
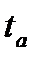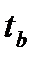3) Найдите критическое значение коэффициента Стьюдента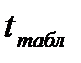 
. Выделите клетку, в которой вы хотите разместить значение 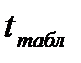. Выполните последовательно процедуры: Вставка-функция - статистические-СТЬЮДРАСПОБР. Введите значения уровня значимости 
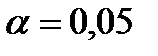и числа степеней свободы 
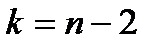. Нажмите ОК.
4) Сравните данное значение с фактическими значениями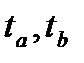 
. Сделайте вывод. Запишите в бланк отчета.
Интервальная оценка коэффициентов линейной регрессии
14. Из столбцов «нижние 95%» и «верхние 95%» таблицы 3 найдите, в каком диапазоне меняются параметры линейной регресси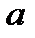и 
и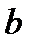 
. Запишите результат.
Выполните пятый пункт. Вычислите прогнозное значение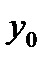 
при прогнозном значении 
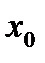, составляющем 110 % от среднего уровня:
15. Найдите среднее значение переменной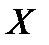 
любым известным для вас способом. Вычислите .
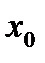16. Подставьте значение 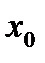в полученное уравнение регрессии. Найдите прогнозное значение зависимой переменной. Запишите результат.
