ЛАБОРАТОРНАЯ РАБОТА № 2
Цель работы: построить на основе статистических данных линейное уравнение регрессии, оценить качество модели, и если она будет удовлетворительной, то сделать прогноз.
ТЕОРИЯ
Оценка статистической значимости уравнения регрессии и его параметров: 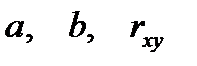 .
.
После того, как найдено уравнение регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
1. О значимости уравнения линейной регрессии в целом можно судить на основании значимости коэффициента корреляции между переменными. Для оценки статистической значимости коэффициента регрессии и корреляции используется 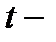 тест.
тест.
Проверяется нулевая гипотеза 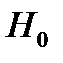 об отсутствии линейной связи между переменными X и Y, т.е.
об отсутствии линейной связи между переменными X и Y, т.е. 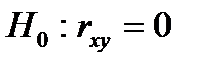 . Конкурирующая гипотеза
. Конкурирующая гипотеза 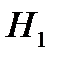 – существует линейная связь между переменными. Проверка нулевой гипотезы состоит в сравнении фактического или наблюдаемого
– существует линейная связь между переменными. Проверка нулевой гипотезы состоит в сравнении фактического или наблюдаемого 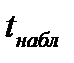 и критического или табличного
и критического или табличного 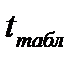 значений
значений 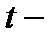 критерия Стьюдента. Рассчитывается
критерия Стьюдента. Рассчитывается 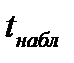 по формуле:
по формуле:
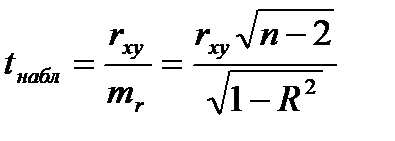 (1)
(1)
Здесь 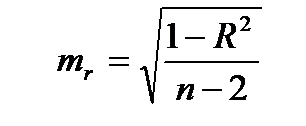 – стандартная ошибка коэффициента корреляции,
– стандартная ошибка коэффициента корреляции, 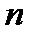 – объем выборки. Полученное значение критерия
– объем выборки. Полученное значение критерия 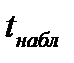 сравнивается с критическим значением
сравнивается с критическим значением 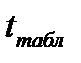 , определяемым по таблице Стьюдента по заданному уровню значимости
, определяемым по таблице Стьюдента по заданному уровню значимости 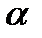 и по числу степеней свободы
и по числу степеней свободы 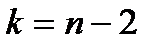 .
.
Уровень значимости 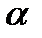 – вероятность отвергнуть правильную нулевую гипотезу, когда она верна (ошибка первого рода). Вероятность того, что будет принята верная нулевая гипотеза называется уровнем надежности и обозначается
– вероятность отвергнуть правильную нулевую гипотезу, когда она верна (ошибка первого рода). Вероятность того, что будет принята верная нулевая гипотеза называется уровнем надежности и обозначается 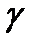 . Надежность и уровень значимости связаны соотношением:
. Надежность и уровень значимости связаны соотношением: 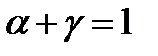 .
.
Если 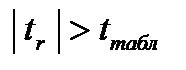 , то гипотеза
, то гипотеза 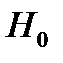 отвергается на уровне значимости
отвергается на уровне значимости 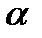 , т.е. считается, что коэффициент корреляции между переменными отличен от нуля
, т.е. считается, что коэффициент корреляции между переменными отличен от нуля 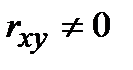 и между переменными существует линейная связь. Уравнение регрессии в данном случае тоже считается значимым.
и между переменными существует линейная связь. Уравнение регрессии в данном случае тоже считается значимым.
Если 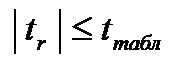 , то мы не можем сделать вывод ни о наличии, ни об отсутствии связи между наблюдаемыми параметрами
, то мы не можем сделать вывод ни о наличии, ни об отсутствии связи между наблюдаемыми параметрами 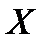 и
и 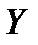 . Необходимо повторить наблюдение на большем количестве наблюдений (данных) и перепроверить гипотезу
. Необходимо повторить наблюдение на большем количестве наблюдений (данных) и перепроверить гипотезу 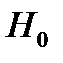 .
.
2. Для оценки статистической значимости найденных МНК параметров уравнения регрессии 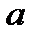 и
и 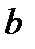 используется
используется 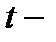 тест.
тест.
Выдвигается нулевая гипотеза 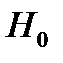 о статистической незначимости, то есть случайной природе показателей. Фактические значения
о статистической незначимости, то есть случайной природе показателей. Фактические значения 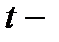 критериев находят по формулам:
критериев находят по формулам:
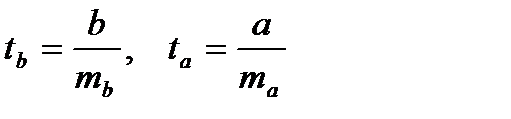 (2)
(2)
Здесь 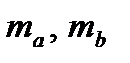 – стандартные ошибки параметров уравнения регрессии и сравнивают с критическим значением
– стандартные ошибки параметров уравнения регрессии и сравнивают с критическим значением 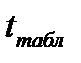 , определяемым по таблице Стьюдента по заданному уровню значимости
, определяемым по таблице Стьюдента по заданному уровню значимости 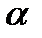 и по числу степеней свободы
и по числу степеней свободы 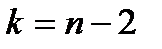 .
.
Величину стандартных ошибок можно определить по формулам:
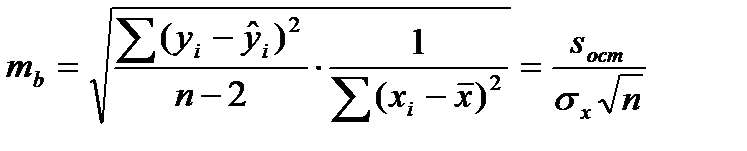 (3)
(3)
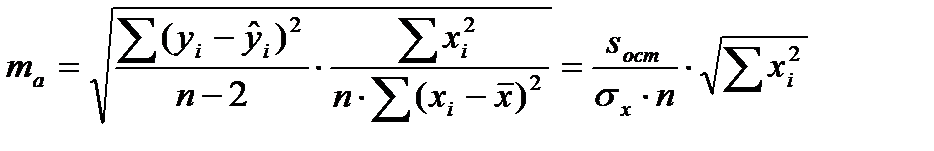 , (4)
, (4)
где 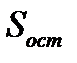 – стандартная ошибка. Если наблюдаемые значения
– стандартная ошибка. Если наблюдаемые значения 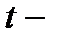 критерия
критерия 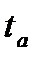 и
и 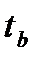 больше табличного значения
больше табличного значения 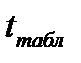 , то гипотеза
, то гипотеза 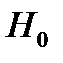 отклоняется, т.е. параметры
отклоняется, т.е. параметры 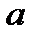 и
и 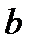 не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора
не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора 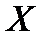 . Уравнение регрессии в данном случае тоже считается значимым.
. Уравнение регрессии в данном случае тоже считается значимым.
Если 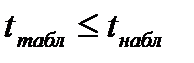 , то мы не можем сделать вывод ни о наличии, ни об отсутствии связи между наблюдаемыми параметрами. Необходимо повторить наблюдение на большем количестве наблюдений (данных) и перепроверить гипотезу.
, то мы не можем сделать вывод ни о наличии, ни об отсутствии связи между наблюдаемыми параметрами. Необходимо повторить наблюдение на большем количестве наблюдений (данных) и перепроверить гипотезу.
3. Оценка статистической значимости уравнения в целом проводится с помощью 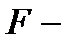 критерия.
критерия.
Общая сумма квадратов отклонений переменной 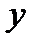 от среднего значения
от среднего значения 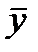 раскладывается на два слагаемых: «объясненную» (факторную) и «остаточную» («необъясненную») сумму квадратов:
раскладывается на два слагаемых: «объясненную» (факторную) и «остаточную» («необъясненную») сумму квадратов:
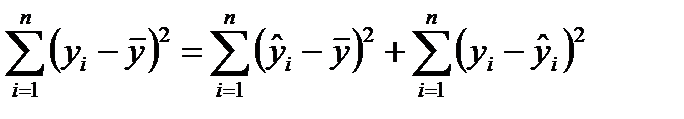 (5)
(5)
Любая сумма квадратов отклонений связана с числом степеней свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант.
Для общей сумы квадратов 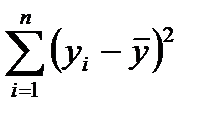 необходимо
необходимо 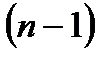 независимых отклонений, поскольку в совокупности из n единиц после расчета среднего уровня свободно варьируются лишь
независимых отклонений, поскольку в совокупности из n единиц после расчета среднего уровня свободно варьируются лишь 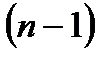 число отклонений. Например, ряд значений y: 1, 2, 3, 4, 5. Среднее из них равно 3, и тогда n отклонений от среднего составят -2, -1, 0, 1, 2. Поскольку
число отклонений. Например, ряд значений y: 1, 2, 3, 4, 5. Среднее из них равно 3, и тогда n отклонений от среднего составят -2, -1, 0, 1, 2. Поскольку 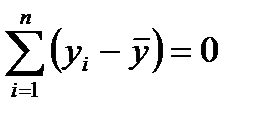 , то свободно варьируют лишь четыре отклонения, а пятое может быть определено, если четыре предыдущих известно.
, то свободно варьируют лишь четыре отклонения, а пятое может быть определено, если четыре предыдущих известно.
Факторная сумма квадратов отклонений для парного линейного уравнения регрессии имеет число степеней свободы, равное 1, поскольку при заданном объеме наблюдений по x и y факторная сумма квадратов зависит только от одной константы – коэффициента регрессии b.
Число степеней свободы остаточной суммы квадратов составляет 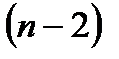 . Таким образом, для степеней свободы имеем равенство:
. Таким образом, для степеней свободы имеем равенство:
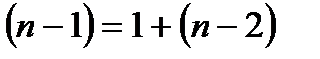 (6)
(6)
Разделив каждую суму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы:
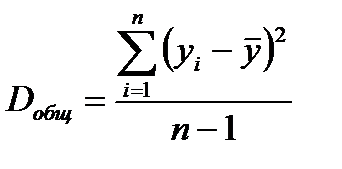 (7)
(7)
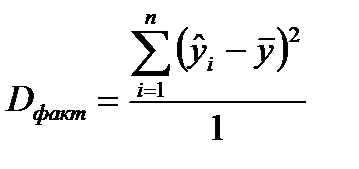 (8)
(8)
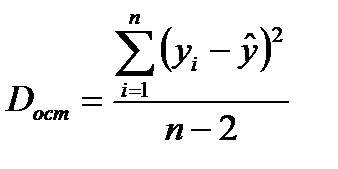 (9)
(9)
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточные дисперсии в расчете на одну степень свободы, получим величину 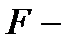 критерия:
критерия:
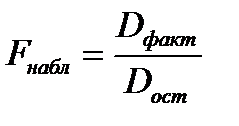 (10)
(10)
Величина 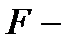 критерия связана с коэффициентом детерминации
критерия связана с коэффициентом детерминации 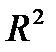 . Факторную сумму квадратов отклонений можно представить следующим образом:
. Факторную сумму квадратов отклонений можно представить следующим образом:
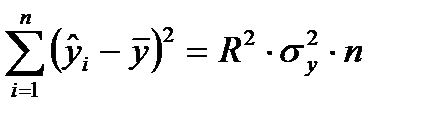 , (11)
, (11)
а остаточную суму квадратов:
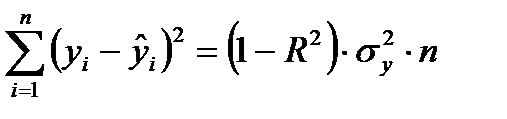 (12)
(12)
На основе формул (8)-(12) можно записать:
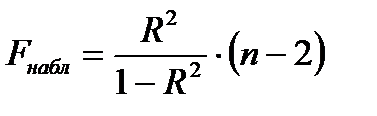 (13)
(13)
При проверки статистической значимости уравнения регрессии с помощью критерия Фишера проверяется нулевая гипотеза 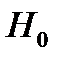 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического 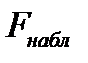 и табличного
и табличного 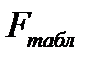 значений критерия Фишера.
значений критерия Фишера. 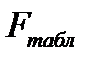 определяется из специальной таблицы с помощью трех чисел: уровня значимости
определяется из специальной таблицы с помощью трех чисел: уровня значимости 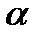 и степеней свободы
и степеней свободы 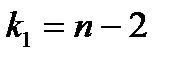 и
и 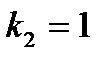 .
.
Нулевая гипотеза отклоняется, если 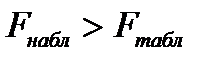 и признается статистическая значимость и надежность оцениваемых характеристик. Если
и признается статистическая значимость и надежность оцениваемых характеристик. Если 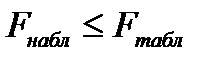 , то гипотеза
, то гипотеза 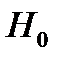 не отклоняется и признается статистическая незначимость уравнения регрессии.
не отклоняется и признается статистическая незначимость уравнения регрессии.
В экономических исследованиях широкое применение находит такой показатель как коэффициент эластичности, вычисляемый по формуле:
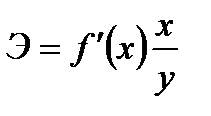 (14)
(14)
Коэффициент эластичности показывает, на сколько процентов изменится результат 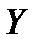 при изменении фактора
при изменении фактора 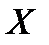 на 1 % от своего номинального значения. Для линейной регрессии коэффициент эластичности равен:
на 1 % от своего номинального значения. Для линейной регрессии коэффициент эластичности равен:
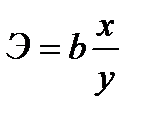 (15)
(15)
и зависит от 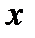 , поэтому рассчитывают средний коэффициент эластичности по формуле:
, поэтому рассчитывают средний коэффициент эластичности по формуле:
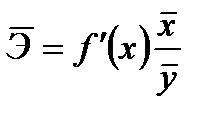 (16)
(16)
Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат 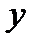 от своей величины при изменении фактора
от своей величины при изменении фактора 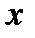 на 1 % от своего значения.
на 1 % от своего значения.
Оценка параметров уравнения регрессии производится на основании конечного числа статистических данных, поэтому сами коэффициенты уравнения регрессии являются случайными величинами, изменяющимися от выборки к выборке. Более правильно, с этой точки зрения, характеризовать параметр не только числовым значением (рассчитанным, например, по МНК), а доверительным интервалом, который покрывает параметр с некоторой (заданной заранее) вероятностью.
Пусть дана линейная регрессионная модель 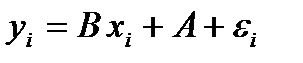 , для параметров которой (A и B) найдены оценки (a и b). Тогда числовые интервалы, покрывающие неизвестные параметры (A и B) с вероятностью
, для параметров которой (A и B) найдены оценки (a и b). Тогда числовые интервалы, покрывающие неизвестные параметры (A и B) с вероятностью 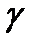 определяются формулами:
определяются формулами:
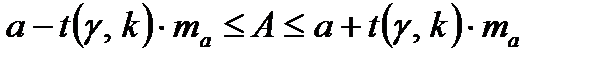 , (17)
, (17)
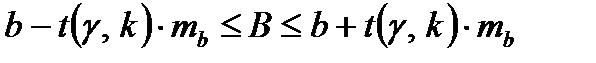 , (18)
, (18)
где – 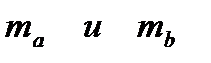 – стандартные ошибки параметров уравнения регрессии, a и b – значения параметров уравнения регрессии, найденные каким-либо способом (например, МНК),
– стандартные ошибки параметров уравнения регрессии, a и b – значения параметров уравнения регрессии, найденные каким-либо способом (например, МНК), 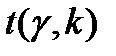 – коэффициент Стьюдента для данного уровня надежности
– коэффициент Стьюдента для данного уровня надежности 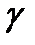 (или данного уровня значимости
(или данного уровня значимости 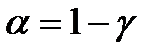 ) и
) и 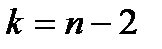 – число степеней свободы, n – объем выборки, т.е. число имеющихся пар данных.
– число степеней свободы, n – объем выборки, т.е. число имеющихся пар данных.
Под прогнозированием в эконометрике понимается построение оценки зависимой переменной для некоторого набора независимых переменных, которых нет в исходных наблюдениях.
Различают точечное и интервальное прогнозирование. В первом случае оценка – некоторое число, а во втором – интервал, в котором находится истинное значение зависимой переменной с заданным уровнем значимости.
Пусть 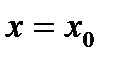 значение воздействующего фактора. Тогда предсказанным значением является оценка
значение воздействующего фактора. Тогда предсказанным значением является оценка 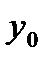 (точечный прогноз), величину которой найдем из уравнения регрессии
(точечный прогноз), величину которой найдем из уравнения регрессии 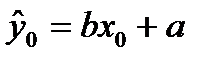 .
.
Ошибка предсказания равна разности между предсказанным и действительным значениями результативного признака: 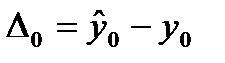 .
.
Ошибка предсказания оценивается по формуле: 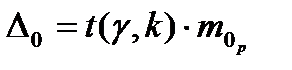 , здесь
, здесь 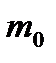 – стандартная ошибка предсказания, вычисляемая по формуле:
– стандартная ошибка предсказания, вычисляемая по формуле:
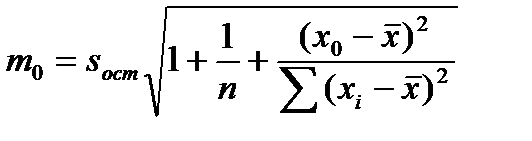 . (19)
. (19)
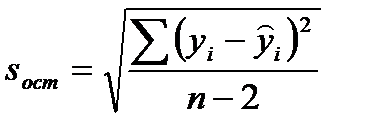 (20)
(20)
Соответствующий доверительный интервал (интервал прогноза) для прогнозов индивидуальных значений 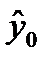 будет определяться по формуле:
будет определяться по формуле:

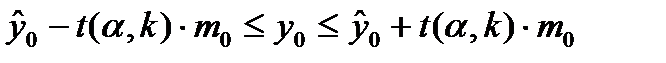 (21)
(21)
Анализ формулы стандартной ошибки предсказания показывает: ширина доверительного интервала является переменной величиной. Она минимальна при 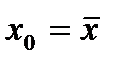 и чем больше
и чем больше 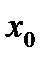 отклоняется от выборочного среднего
отклоняется от выборочного среднего 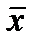 , тем больше величина ошибки; чем больше объем выборки
, тем больше величина ошибки; чем больше объем выборки 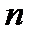 , тем величина ошибки меньше. Прогноз значений по уравнению регрессии оправдан, если значение объясняющей переменной не выходит за диапазон ее значений по выборке, поэтому экстраполяция кривой регрессии может привести к значительной погрешности.
, тем величина ошибки меньше. Прогноз значений по уравнению регрессии оправдан, если значение объясняющей переменной не выходит за диапазон ее значений по выборке, поэтому экстраполяция кривой регрессии может привести к значительной погрешности.
ПОСТАНОВКА ЗАДАЧИ
По территориям региона приводятся данные 199Х г.
| Номер региона | ||||||||||||
| Среднедушевой прожиточный минимум, в день одного трудоспособного, руб., х | ||||||||||||
| Среднедневная заработная плата, руб, у |
1. найти параметры 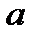 и
и 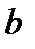 линейного уравнения парной регрессии
линейного уравнения парной регрессии 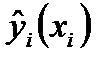 ;
;
2. найти коэффициент детерминации;
3. рассчитать линейный коэффициент парной корреляции и оценить тесноту связи, используя таблицу Чеддока;
4. оценить статистическую значимость параметров уравнения регрессии, используя 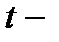 статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей с 95% надежностью;
статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей с 95% надежностью;
5. вычислить прогнозное значение 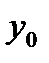 при прогнозном значении
при прогнозном значении 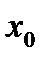 , составляющем 110 % от среднего уровня;
, составляющем 110 % от среднего уровня;
6. оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал;
7. полученные результаты изобразить графически и привести экономическое обоснование.
 2015-05-10
2015-05-10 1104
1104