Построение математической модели задачи:
Формулировка математической модели задачи:
1) переменные для решения задачи. x1 - суточный объем производства материала А, Х2 - суточный объем производства материала В;
2) определение функции цели (критерия оптимизации). Суммарная суточная прибыль от производства X1 материала А и x 2 материала В равна: 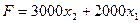 поэтому цель фабрики - среди всех допустимых значений х1 и х2 найти такие, которые максимизируют суммарную прибыль от производства материалов.
поэтому цель фабрики - среди всех допустимых значений х1 и х2 найти такие, которые максимизируют суммарную прибыль от производства материалов.
ограничения на переменные:
а) объем производства материалов не может быть отрицательным, т.е. 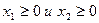 .
.
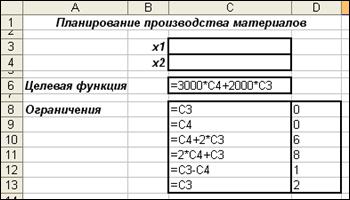 б) расход исходного продукта для производства обоих видов материалов не может превосходить максимально возможного заданного исходного продукта, т.е.
б) расход исходного продукта для производства обоих видов материалов не может превосходить максимально возможного заданного исходного продукта, т.е. 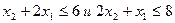 .
.
в) ограничения на величину спроса на материалы: 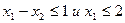
Таким образом получаем следующую математическую модель задачи:
Найти максимум функции: 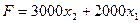
При ограничениях: 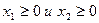 ,
, 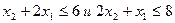 ,
, 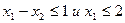 .
.
 2015-05-10
2015-05-10 1261
1261








