Краткие теоретические сведения. Тема: Исследование режимов работы длинной линии

Лабораторная работа №6

Тема: Исследование режимов работы длинной линии

Цель: Научить задавать различные режимы работы длинных линий, анализировать полученные распределения токов и напряжений, делать выводы из полученных результатов.

Оборудование: ПЭВМ со специализированным пакетом программ NI LabVIEW.

Краткие теоретические сведения

Длинные линии (ДЛ) относятся к цепям с распределенными параметрами, где параметры r, L, С распределены и неотделимы один от другого.

ДЛ – это система проводов, у которых длина l соизмерима с длиной волны λ, распространяемых вдоль линии электромагнитных колебаний или значительно больше ее.

Схема подключения двухпроводной ДЛ к генератору с напряжением 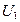и к нагрузке 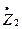показана на рисунке1.

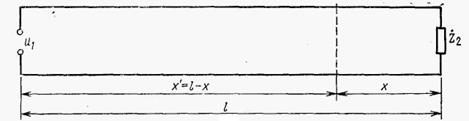
Рисунок 2.7.1 – Схема подключения ДЛ

На рисунке 2.7.1 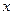- расстояние от конца линии до произвольного участка, 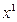- расстояние от начала линии до произвольного участка.

Любой элементарный участок линии длинной dx обладает индуктивностью dL, активным сопротивлением проводов dR, емкостью dC и активной проводимостью dG (утечкой) между проводами.

Следовательно, двухпроводная линия – это цепь с распределенными параметрами. На каждую единицу ее длины приходятся так называемые погонные параметры линии:

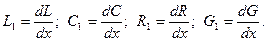(1)

Линия называется однородной, если погонные параметры одинаковы на всем ее протяжении.

Полное погонное сопротивление проводов 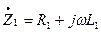, а полная погонная проводимость между проводами 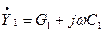. На высоких частотах, когда 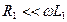и 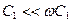нередко пренебрегают потерями 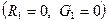и тогда линию считают идеальной.

При анализе процессов, происходящих в линии, удобно пользоваться эквивалентной схемой длинной линии, показанной на рисунке 2.

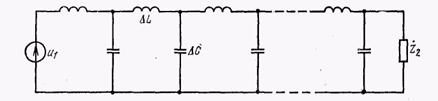
Рисунок 2 – Эквивалентная схема длинной линии

Эквивалентная схема учитывает, что индуктивности полностью включены в верхний провод линии и позволяют рассматривать ДЛ как идеальную, состоящую и большого числа звеньев – фильтров нижних частот. Тогда можно определить волновое сопротивление 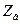линии с распределенными параметрами в виде

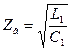. (2)

Как видно волновое сопротивление линии без потерь чисто активное и не зависит от частоты.

Мгновенное значение тока неодинаково в разных сечениях линии.

Временные изменения напряжения 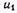и тока 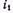на зажимах генератора повторяются вдоль линии с запаздыванием, тем большим, чем больше координата х'. Поэтому пространственные диаграммы бегущей волны совпадают по форме с временной диаграммой на­пряжения 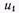и тока 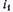генератора.

В цепях с распределенными параметрами величины и и i –функции двух независимых переменных: времени t и пространственной координаты х' (или х).

Отставание по фазе к концу линии 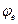жестко связано с ее длиной 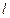, скоростью распространения бегущей волны 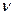и длиной волны 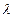. Эта связь устанавливается через коэффициент фазы (волновое число) 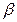, выражающий разность фаз на концах отрезка длиной в одну единицу длины. При 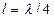угол 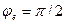, откуда

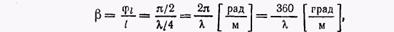(3)

но так как , то

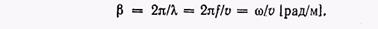(4)

Если линия замкнута на сопротивление 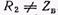, то нагрузка не может полностью поглотить энергию падающей волны. Пусть, например, волновое сопро­тивление идеальной линии 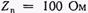, сопротивление нагрузки 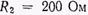и напряжение источника постоянно и равно 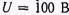. Тогда ток па­дающей волны . Но при напря­жении 100 В такой ток через нагрузку пройти не может, так как 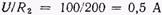. Не поглощенная нагрузкой часть тока будет подзаряжать конечную элементарную емкость линии до на­пряжения, большего чем 100 В, от нее зарядится предпоследняя емкость и т. д. Из-за этого в линии создается обратная – отраженн ая волна с не поглощенным током (0,5 А) и мощностью, равной разности поступившей от генератора и поглощенной в нагрузке.

Отраженная волна аналогична падающей: ее можно рассматри­вать как результат того, что емкости элементарных участков заря­жаются через индуктивности участков, но в обратном порядке – от конца линии к ее началу. Таким образом, при произвольной на­грузке через любое сечение линии проходят две встречные бегущие волны – падающая и отраженная. Если падающая и отраженная волны одинаковы по интенсивности, то переноса энергии нет и ре­зультирующая волна называется стоячей. При неодинаковой ин­тенсивности встречных волн образуются смешанные волны, т. е. совокупность бегущей и стоячей волн.

Теперь можно дать полное определение чисто бегущей волны: это такая волна, которая в процессе распространения нигде не пре­терпевает отражения, для чего линия передачи должна быть одно­родной и сопротивление нагрузки должно быть активным и равным волновому сопротивлению линии. Отсюда следует, что характер волн в линии определяется, прежде всего, отношением сопротив­ления нагрузки к волновому сопротивлению линии. Из этих сообра­жений во многих случаях место расположения данного сечения линии выражают расстоянием х от ее конца.

Таким образом однородная линия на всем протяжении представляет для бегущей волны напряжения активное сопротивление, равное волновому z_B, поэтому, когда сопротивление нагрузки Z₂ = R₂ = Z_B, условия распространения падающей волны при достижении ею нагрузки не нарушаются и передаваемая по линии энергия полностью поглощается в сопротивлении R₂. Напряжение U_x и ток 1_Х бегущей волны не изменяются вдоль идеальной линии (рисунок3).

Если линия без потерь на конце разомкнута (Z₂ ->∞), замкнута накоротко (Z₂=0) или на реактивное сопротивление (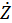 ₂=jX₂,),то энергия не поглощается не только в линии, но и в нагрузке. Образуются падающая и отраженная волны равной интенсивности; складываясь геометрически, они создают чисто стоячие волны, в которых максимумы (пучности) и нули (узлы) величин U_x и 1_Х фиксируются в определенных сечениях линии (рисунок 3).

Если нагрузкой линии (в том числе идеальной) является активное сопротивление, не равное волновому (Z₂ = R₂>Z_в, Z₂ =R₂ <Z_в), или комплексное сопротивление (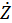 ₂ = R₂ + jX₂), то в линии существуют смешанные волны, при которых U_xmin не равно 0, и I_xmin не равно 0 (рисунок 3).

В реальной линии (R1 не равно 0,(G1 не равно 0), независимо от характера нагрузки,существует некоторая бегущая волна, обусловленная потерями энергии в линии. Например, в реальной согласованной линии (Z₂ = Z_B) и напряжение U_x и ток I_х затухают по экспоненте к концу линии (рисунок 3).

5. Всякая согласованная линия нерезонансная, ее эквивалентное сопротивление по всей длине линии одинаковое и равно волновому Z_B. Входное сопротивление линии, работающей в режиме стоячих волн, реактивное (Х_вх), оно делает линию эквивалентной колебательному контуру без потерь, настроенному в резонанс или расстроенному. В первом случае на входе линии наблюдаются пучности и узлы напряжения и тока, а Х_вх = 0, ± 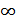. Если же линия работает в режиме смешанных волн, то реактивная составляющая Х_вх, обусловленная стоячей волной, дополняется активной составляющей R_BX, обусловленной бегущей волной, и входное сопротивление линии комплексное: 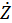_BX = R_bx + jX _BX (рисунок 3).

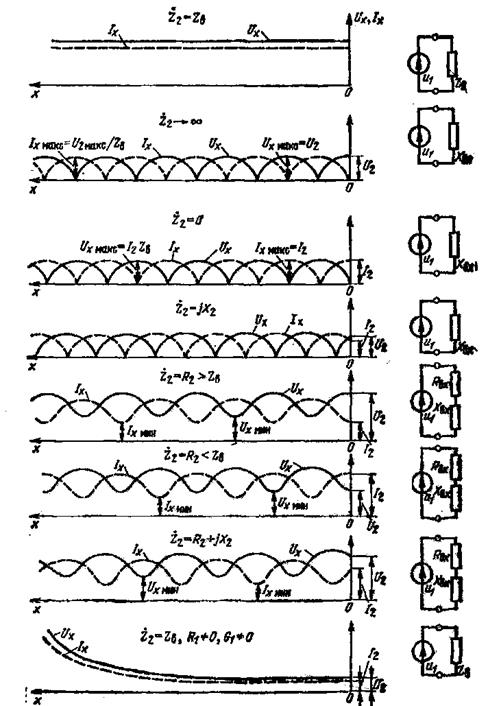
Рисунок 3 –2.7.18 - Распределение действующих значений напряжения и тока вдоль идеальной и реальной (R₁≠0,G₁≠0) линий при различных значениях сопротивления нагрузки Z₂.