Двухпроводная линия передачи

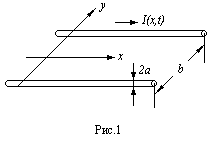
В настоящей работе мы рассмотрим вопросы, связанные с распространением волн в двухпроводной линии передачи. Она образована двумя цилиндрическими проводниками (рис.1), находящимися в среде с диэлектрической проницаемостью 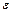и магнитной проницаемостью 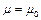( 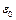и 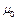- соответствующие параметры для вакуума). Радиусы проводников 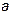и расстояние между их осями 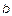малы по сравнению с длиной волны 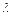. Анализируется только противофазный режим, когда токи в проводниках 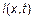одинаковы по величине, но текут в противоположных направлениях.

Единица длины линии обладает определенными параметрами: индуктивностью 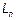, емкостью 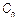,сопротивлением проводов 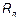и проводимостью среды (утечкой) 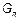. Их называют погонными параметрами линии. Приближенные формулы для них выводятся и обсуждаются в приложении.

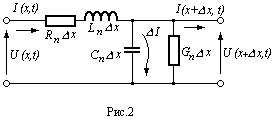
Для отрезка линии длиной 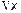мы можем изобразить такую эквивалентную схему (рис.2) и написать уравнения Кирхгофа.

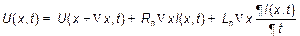
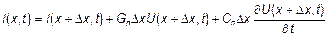
Их надо поделить на 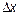и сделать предельный переход 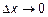. Тогда мы получим систему дифференциальных уравнений, приближенно описывающих процесс распространения волн в линии и называемых телеграфными уравнениями.

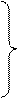
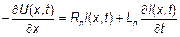
(1)

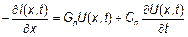
Слово "приближенно" подчеркивает, что эта система (как и теория цепей) не учитывает излучение энергии в окружающее пространство при формировании (главным образом) и распространении волн. Однако, если 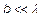, то излученная энергия составляет ничтожную часть от передаваемой, и излучение можно не учитывать.

Исключая из системы ток или напряжение, мы для оставшейся величины получим волновое уравнение. Особенно простое оно по 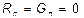лучается, если пренебречь тепловыми потерями, т.е. считать 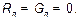Напишем уравнение для напряжения (для тока оно такое же).

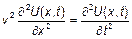, где .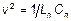

Общим решением волнового уравнения как легко проверить) является сумма двух функций 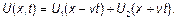Они описывают волновые возмущения, распространяющиеся по линии без затухания со скоростью 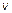в противоположных направлениях. Конкретный вид функци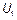й и 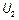определяется начальными условиями (условиями возбуждения), но не уравнением. Отметим интересный результат. При отсутствии тепловых потерь в среде и проводах скорость распространения волн определяется только свойствами среды, и не зависит от геометрических параметров линии, так как 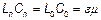(выражения 1 и 2 приложения).

При наличии тепловых потерь в линии и среде, волны будут затухать по мере распространения и замедляться. Появится дисперсия (частотная зависимость коэффициентов затухания и замедления) и, как следствие, искажение формы сигнала в процессе распространения. Это и составляет предмет исследования в данной работе.

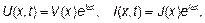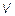Рассмотрим подробнее распространение импульса в линии с потерями, используя спектральный подход. В качестве первого шага на этом пути, надо рассмотреть распространение волнового возмущения с гармонической зависимостью от времени. Пусть где и 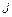- комплексные амплитуды напряжения и тока. Для них телеграфные уравнения запишутся так:

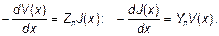(2) Здесь 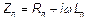и 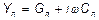представляют комплексные сопротивление и проводимость единицы длины линии. Исключая ток из системы, получим:

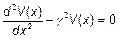, (3) где 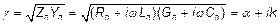(4) - постоянная распространения (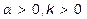). Величину 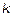называют волновым числом.

Последнее уравнение достаточно простое, часто встречается в физических задачах и хорошо изучено. Напишем сразу его решение.

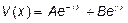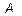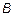. (5) Здесь и - комплексные постоянные, которые определяются из граничных условий на концах линии. Тогда для тока получим следующее выражение:
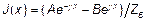(6) где 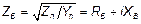- волновое или характеристическое сопротивление линии (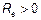). Оно определяется как отношение напряжения к току для одной бегущей волны.

Запишем решение с учетом временного множителя. Так нагляднее видны структура и физический смысл слагаемых решения.

.

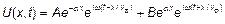Здесь 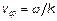- фазовая скорость распространения волн. Первое слагаемое описывает гармоническое возмущение, распространяющееся по линии со скоростью 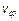в направлении оси 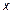. Постоянная 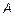определяет амплитуду этой волны при 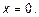Но, в целом, амплитуда не постоянна, а убывает с расстоянием по мере распространения волны по экспоненциальному закону за счет множителя 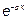. Параметр 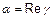называют коэффициентом затухания; на длине 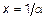волна убывает в 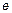раз. Второе слагаемое представляет аналогичную волну, бегущую в обратном направлении. Пусть линия длиной 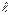возбуждается слева (при 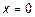) генератором напряжения 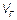с внутренним сопротивлением 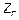и нагружена на конце (при 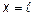) сопротивлением 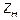(рис. 3).

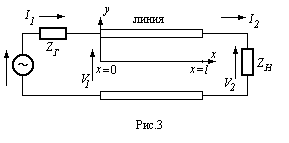
Тогда волну, бегущую от генератора (первое слагаемое в решении) называют прямой или падающей. Другую волну называют отраженной. Отражения могут возникать только в местах нарушения однородности линии (конец линии, нагрузка, изгибы, разветвления, изменения размеров 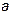или ).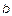

Определим входное сопротивление линии и коэффициент передачи отрезка линии длиной .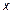

Имеем: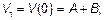

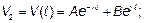
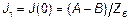
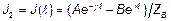
На конце линии 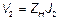. Подставляя сюда 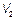и 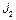, получим соотношение между 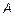и 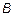: 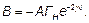Величину 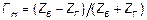называют коэффициентом отражения от нагрузки (по току). Тогда:

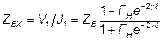, (7)

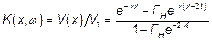. (8)

Полезно написать еще формулу, связывающую 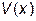и ЭДС генератора .

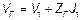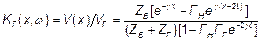. (9)

Здесь 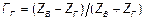- коэффициент отражения на входе линии, от генератора.

Если 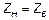, то линия оказывается идеально согласованной, и отражений нет (бесконечная однородная линия). При этом: 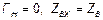и

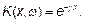(10)

В линии останется только падающая волна. Такую ситуацию мы прежде всего и рассмотрим.

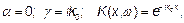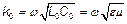Для линии без потерь: где - волновое число среды. Дисперсии нет, импульс не ослабляется, не искажается, только запаздывает на время распространения 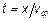. При этом волновое сопротивление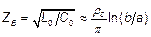 активно и постоянно. Величина 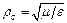есть волновое сопротивлениесопротивление среды. Для вакуума 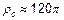Ом.

Для линии с потерями параметр 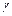комплексный и зависит от частоты 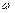более сложным образом. Дисперсия есть, импульс задерживается, ослабляется и искажается по мере распространения. Частота 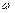входит в параметр 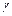явно, а также неявно, поскольку сами погонные параметры 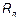, 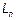и другие зависят от частоты. Обсудим это подробнее.

Вычисление погонных параметров линии в широком диапазоне частот представляет сложную электродинамическую задачу по двум причинам. Первая, это скин-эффект, который приводит к перераспределению тока по сечению проводников, к "вытеснению" тока к поверхности проводника с ростом частоты. Вторая причина заключается в нарушении осевой симметрии распределения тока и заряда в проводнике, за счет влияния одного провода на другой. Например, заряд на поверхности проводника будет неравномерно распределен по периметру. Чем меньше расстояние между проводами, тем сильнее будет выражен этот эффект.

Нас интересуют, прежде всего, качественные результаты, и высокая точность не нужна. Поэтому в приложении получены приближенные выражения для погонных параметров линии. Здесь мы приведем только результаты с краткими комментариями.

Обычно потери энергии в проводах больше чем потери окружающей среде. Учтем только первые и положим .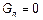

Зависимость емкости 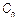от частоты для металлических проводников чрезвычайно слабая в рассматриваемом диапазоне частот. Не будем ее учитывать и примем 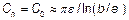, т.е. статической емкости проводов (формула 1 приложения).

Сопротивление проводников с ростом частоты увеличивается за счет скин-эффекта, поскольку глубина проникновения поля и тока в проводник уменьшается. При сильно выраженном скин-эффекте ток убывает экспоненциально по мере удаления от поверхности проводника. Убывание в 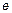раз происходит на расстоянии 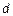, условно называемом толщиной скинслоя. Электродинамический расчет дает для этой величины следующее значени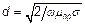е: ,где 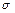- удельная проводимость провода, а 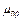- его магнитная проницаемость. В итоге (формулы 3 и 4 приложения):

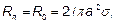
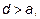(11)

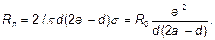
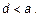
Таким образом, при сильном скин-эффекте (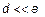) сопротивление 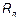растет пропорционально .

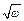Теперь обратимся к индуктивности. Она определяется или из энергетических соображений, или как коэффициент, связывающий ток в контуре с потоком магнитной индукции, пронизывающим этот контур. Поток индукции реализуется как внутри проводов, так и вне их. Соответственно различают индуктивность внутреннюю и внешнюю.

Внешняя индуктивность 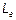слабо зависит от распределения тока внутри проводников и от частоты. Ее можно принять такой, как для идеальных проводников (формула 2 приложения). .

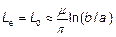Внутренняя индуктивность с учетом скин-эффекта такова (формулы 5 и 6 приложения):

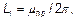
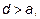(12)

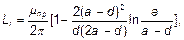
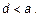
Для идеально проводящих проводников внутренняя индуктивность 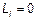(поля внутри нет). К этому мы приходим с ростом частоты и в реальных проводниках, так как токи вытесняются к поверхности проводников и 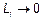, когда 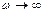(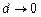). Однако, индуктивное сопротивление 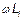при этом растет, как 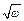. Отметим интересный предельный результат, который легко получается путем разложения выражения для 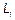в ряд при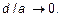 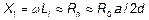, причем всегда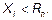

Общая индуктивность 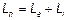. Соответственно, полное индуктивное сопротивление 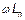на высоких частотах растет пропорционально частоте, за счет внешней индуктивности. Поэтому, при 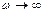будет выполняется неравенство 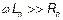. Приведенные в табл. 1 и 2 приложения оценки дают представление о величинах обсуждаемых параметров для медных и железных проводов.

Теперь мы можем перейти непосредственно к анализу искажений импульса в согласованной линии. Какие искажения импульса следует ожидать? Сначала обсудим это на качественном уровне.

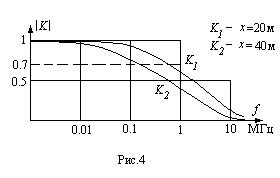
Изображенная на рис. 2 схема отрезка линии малой длины, представляет типичную ячейку фильтра нижних частот. Вычисления 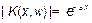подтверждают это. На рис.4 приведены две зависимости 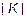от частоты для отрезков линий длиной 20 и 40 метров с железными проводниками (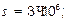 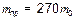). Это типичные характеристики фильтров нижних частот. Чем длиннее отрезок линии, тем меньше граничная частота фильтра и тем быстрее убывает 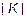с частотой. Для медных проводников затухание значительно меньше, поэтому в указанном диапазоне частот и расстояний, оно проявляется еще очень слабо.

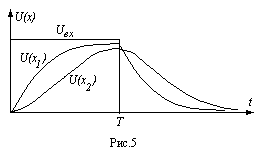
Пусть на входе линии мы имеем прямоугольный импульс длительности 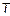(рис. 5). При малой длине линии искажения будут очень похожи на искажения импульса в инте-грирующей цепочке, при условии, что постоянная времени цепочки меньше или порядка длительности импульса (кривая 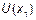). По мере увеличения длины линии, длительность фронтов будет расти (граничная частота фильтра убывает), а резкие изменения (изло-мы) будут становиться более плавными (гладкими), как для двух, трех-звенной интегри-рующей цепи (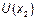). Аккуратные вычисления целиком подтверждают эти качествен-ные соображения.

Напомним алгоритм спектрального метода. Спектр входного прямоугольного импульса с "амплитудой" 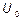и длительностью 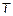хорошо известен:

.

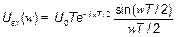Коэффициент передачи 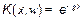отрезка согласованной линии мы определили. Тогда, спектр сигнала в линии получается перемножением этих функции. 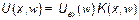. Наконец, сам сигнал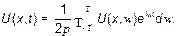

Все сводится к вычислению этого интеграла Фурье.

Результаты вычислений для железных проводников изображены на приведенных рисунках для двух расстояний и длительностей импульса. Рисунки анализируются парами. На первых, для удобства сравнения, приведены нормированные частотные зависимости модулей коэффициента передачи отрезка линии и плотности спектра входного импульса, на других - временные, т.е. форма сигнала в линии.

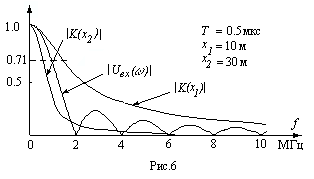
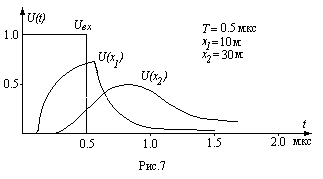
Первая пара (рис. 6 и 7) соответствует случаю сравнительно длинного импульса (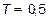 мкс.). На малом расстоянии 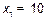м. (кривые 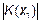и 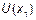) полоса пропускания отрезка линии (на уровне 0,71) порядка ширины спектра импульса до первого нуля огибающей (так обычно оценивается ширина спектра импульса). Сильно ослабляются только высокочастотные составляющие спектра, и это приводит, в основном, к искажению фронта импульса. На рис. 7 четко видна задержка сигнала (на качественных рисунках она не отражена). С увеличением расстояния 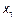до 30 м.

(кривые 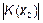и 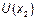) полоса пропускания отрезка линии становится значительно уже и возрастает скорость убывания 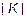с ростом частоты. В результате, импульс

получился более растянутым, сглаженным. Нарастание сигнала после его появления

идет гораздо медленнее, да и сам момент появления стал менее четким.

Вторая пара рисунков (8 и 9) иллюстрирует более сильное искажение импульса на малых расстояниях (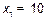 м.) при уменьшении длительности импульса до 0,1 мкс. Спектр импульса стал в 5 раз шире. Теперь сильно ослабляются и спектральные составляющие в пределах главного максимума спектральной плотности импульса. Начало временного процесса такое же, как на рис. 7 (кривая 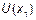; реакция на ступеньку напряжения одинакова), только спад начинается значительно раньше. Искажения

импульса становятся более значительными. Все отмеченные особенности искажения импульса можно реально наблюдать на макете линии.