Определение критической температуры

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

КАФЕДРА МОЛЕКУЛЯРНОЙ ФИЗИКИ

ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ ТЕМПЕРАТУРЫ

ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ ТЕМПЕРАТУРЫ

I.Краткая теория

§ 1.Реальные газы.

Уравнение состояния Клапейрона - Менделеева достаточно хорошо описывает известные из опытов свойства газов. Однако, оно является приближённым и оказывается справедливым только при достаточно малых давлениях. Кроме того опыт показывает, что при определенных значениях давления и температуры газы конденсируется, т.е. приходят в жидкое состояние. Уравнение Клапейрона - Менделеева это явление не описывает. Изотерма для реального газа при этом имеет характерный вид (рис. 1).

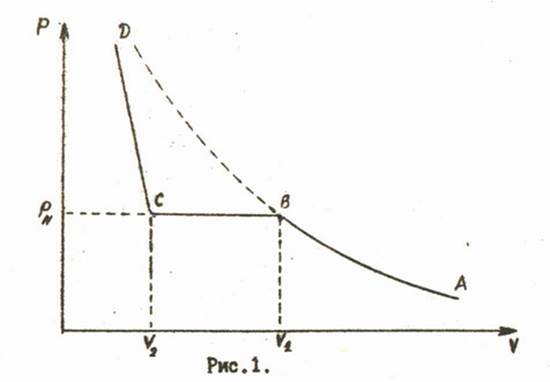
Рассмотрим процесс, соответствующий этому графику, проведённый в направлении ABCD. Часть изотермы AB описывает процесс сжатия газа до начала конденсации. Она достаточно хорошо может совпадать с изотермой, рассчитанной по уравнению Клапейрона-Менделеева (изображена пунктиром). Однако в процессе, проведённом с реальным веществом при определенном давлении начнётся конденсация (точка B на графике). Это давление называют давлением насыщенных паров или просто давлением насыщения .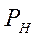

Часть графика BC описывает двухфазное состояние вещества. При уменьшении объема от 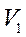до 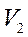все большая доля вещества переходит из парообразного состояния в жидкое. Точка C изображает состояние, когда всё вещество превратилось в жидкость. Наконец, CD описывает процесс сжатия жидкости, график идет почти параллельно вертикальной оси, отражая известный факт: жидкости имеют гораздо меньшую сжимаемость, чем газы.

Если проводить подобные изотермические процессы с одним и тем же количеством вещества при различных температурах, мы получим систему изотерм, изображенную на рис.2.

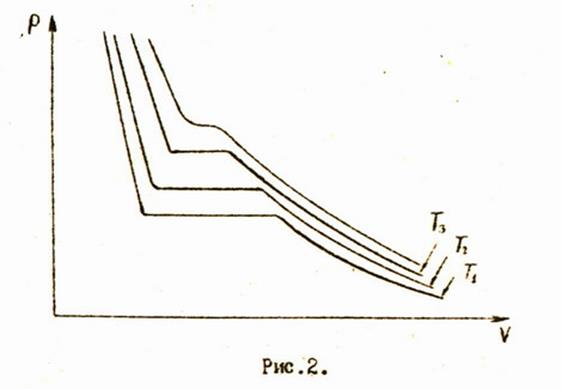
Кривые, соответствующие более высоким температурам, располагаются дальше от начала координат. С повышением температуры горизонтальные части изотерм, описывающие двухфазное состояние, уменьшаются и при некоторой температуре вырождаются в одну единственную точку. Эта температура называется критической.

При температуре выше критической нельзя получить вещество в двухфазном состоянии.

§ 2. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса.

Уравнение состояния идеального газа при больших плотностях не может дать хорошего совпадения с экспериментом, поскольку при eгo написании предполагалось, что молекулы не имеют размеров и не взаимодействуют между собой. Чтобы получить уравнение состояния, удовлетворительно описывающее свойства реальных газов, надо учесть размеры молекул или силы отталкивания, возникающие между молекулами, находящимися на малых расстояниях друг отдруга. Кроме того, надо учестьтакже и силы притяжения между молекулами.

Можно взять за основу уравнение состояния Клапейрона - Менделеева и внести в него соответствующие поправки. Учёт сил отталкивания или размеров молекул произведем, введя поправку к объёму в уравнении Клапейрона - Менделеева для одного киломоля газа

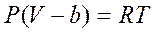(1)

или

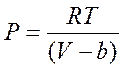(2)

Из второго выражения видно, что при 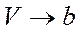давление стремится к бесконечности, т.е. нельзя сжать вещество до объёма, равного нулю.

При сравнительно больших расстояниях междумолекулами существенную роль играют силы притяжения. Их можно учесть, введя соответствующую поправку к давлению в уравнении (2):

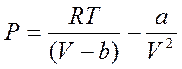(3)

Эту поправку необходимо взять с отрицательным знаком, полагая, что притяжение молекул приводит к уменьшению давления на стенки содержащего данный газ сосуда. Уравнение (3) можно преобразовать так:

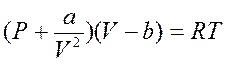(4)

Это и есть уравнение состояния реальных газов, впервые полученное Ван-дер-Ваальсом. Можно записать его для произвольного количества вещества:

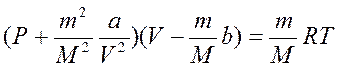(5)

где 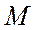относительная молекулярная масса.

Уравнение (4) можно представить в виде степенного ряда по объему:

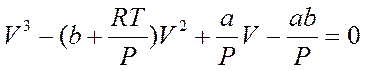(6)

При фиксированных давлении и температуре оно будет являться уравнении третьей степени относительно объема 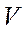и должно иметь три корня. Наиболее интересные результаты получаются при анализе изотерм Ван-дер-Ваальса, одна на которых изображена, на рис.3.

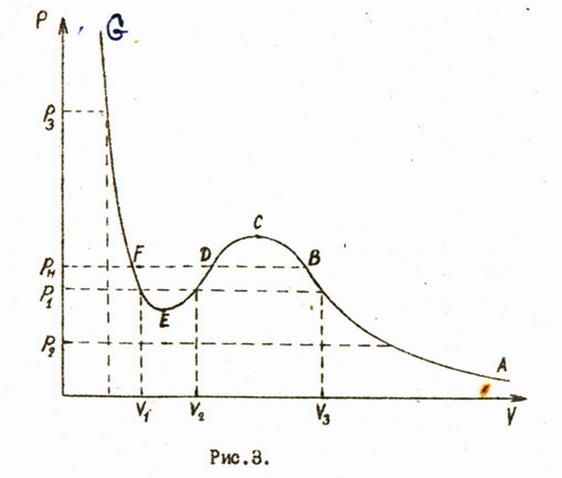
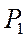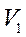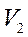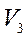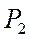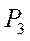При фиксированной температуре каждому значению давление будут соответствовать три корня уравнении (6). Давлению соответствуют три вещественных корня , , . Давлениям и соответствуют один вещественный корень и два комплексно сопряжённых корня, которые физического смысла не имеют и в дальнейшем рассматриваться не будут.

Интересно сопоставить изотерму Ван-дер-Ваальса и опытную изотерму. На рис.3 горизонтальный участок опытной изотермы изображен прямой BF. Часть AB описывает газообразное состояние вещества и удовлетворительно совпадает с опытной изотермой. Часть FG описывает изотермическое сжатие жидкости. Таким образом, уравнение Ван-дер-Ваальса сравнительно неплохо описывает поведение вещества в газообразном и жидком состояниях при изотермическом процессе.

Существенно изотермы отличаются на участке BF. Однако ветви BC и EFимеют определённый физический смысл. Состояния вещества, изображаемые участком BC, могут быть экспериментально получены. Это - пересыщенный или переохлаждённый пар. Состояния вещества, соответствующие участку EFтакже наблюдаются на опыте. Жидкость в таких состояниях называется перегретой. Эти состояния называют метастабильными. Часть изотермы Ван-дер-Ваальса CDE в опытах никогда не наблюдается. Она описывает нестабильное состояние вещества.

§ 3. Критическая температура. Критическое состояние.

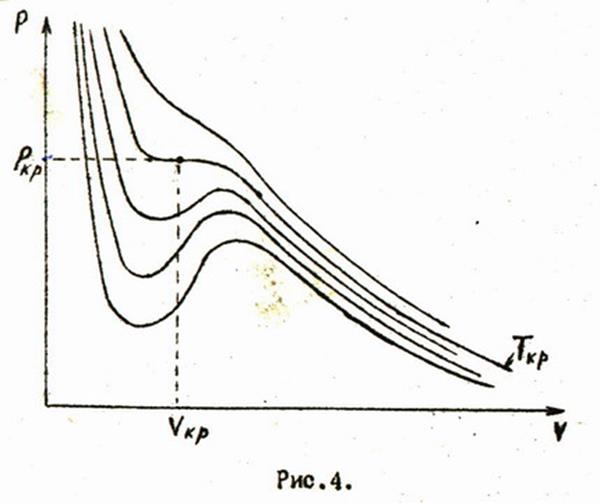
Построим семейство изотерм Ван-дер-Ваальса (рис.4). С увеличением температуры кривые будут располагаться далее от начала координаты и характер их будет меняться. Максимумы и минимумы будут сближаться как по оси абсцисс, так и по оси ординат, и при некоторой температуре сольются в одну точку, точку перегиба. При этой температуре и соответствующем данной точке давлении три вещественных корня становятся кратными. Различие между жидкостью и паром и граница раздела между ними исчезают. Такое состояние называют критическим, а температуру - критической температурой. Эта температура является характерным свойством каждого вещества.

Используя уравнение Ван-дер-Ваальса, можно выразить критические параметры 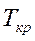, , 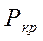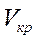через индивидуальные константы вещества 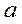и 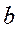, а также через универсальную газовую постоянную .

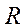Один способ нахождения критических параметров основывается на том, что корни уравнения Ван-дер-Ваальса, написанного для критического состояния, являются кратными, т.е, уравнение можно представить так:

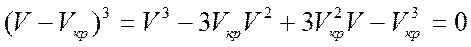(7)

Сопоставим с уравнением (6)

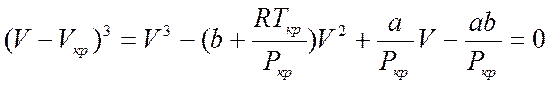
Это равенство будет тождественно выполняться, если коэффициенты, при одинаковых степенях 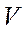будут равны между собой:

,

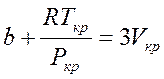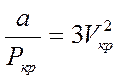, (8)

.

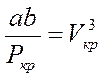Решая систему уравнений (8), получим выражения для критических параметров:

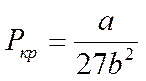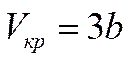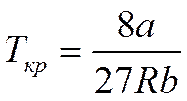, , . (9)

Эти же результаты можно получить другим путем. Как уже отмечалось, точка, изображающая критическое состояние, является точкой перегиба на графике изотермического процесса в координатах 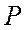, 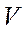. Используем уравнение (3), определяющее давление как функции объёма при фиксированной температуре. Из курса математического анализа известно, что в точке перегиба первая и вторая производные равны нулю:

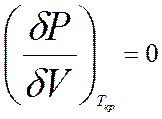(10)

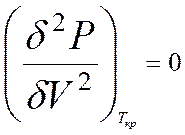(11)

Решая систему уравнений (3), (10), (11) относительно 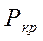, , 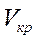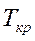получим для них те же соотношения (9).

Определив экспериментально критические параметры, можно найти индивидуальные константы вещества 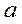и .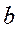

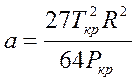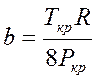, . (12)

Таким образом, уравнение Ван-дер-Ваальса описывает свойства жидкостей и газов, предсказывает существование критического состояния. Однако, оно является менее универсальным, чем уравнение Клапейрона-Менделееве, так как в него входят две индивидуальные константы вещества 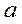и .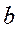

II. Описание УСТАНОВКИ.

Знание критических параметров 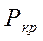, , 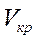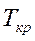представляет значительный научный и практический интерес. При температуре выше критической вещество может существовать только в газообразном состоянии. Скрытая теплота парообразования и коэффициент поверхностного натяжения при критической температуре обращаются в нуль.

Построив на основе экспериментальных данных систему изотерм (как показано не Рис2), можно определить критическую температуру и два других параметра. Этот метод был впервые применен Эндрюсом при определении критических параметров углекислого газ. При определении только критической температуры можно воспользоваться менее громоздким методом исчезновения мениска. Исследуемое вещество помещается в запаянную стеклянную ампулу и нагревается. Если количество жидкости в ампуле подобрано таким образом, что в процессе нагревания мениск практически остается на месте, то в определённый момент вещество достигнет критического состояния (мениск при этом исчезнет). При охлаждении он снова появится и вещество разделится на две фазы. Температура, при которой появляется и исчезает мениск и будет являться критической температурой.

Определение критической температуры производится на установке, схема которой изображена не рис.5.

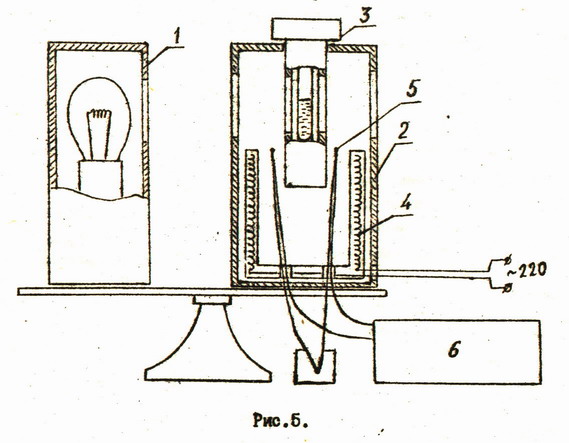
На общей подставке смонтированы осветитель 1 и термостат 2, в который помещается специальный микропресс 3 с исследуемы веществом. В нижней части корпуса осветителя имеется два тумблера: одним включается осветитель, другим нагреватели 4 термостате. Температура термостата контролируется с помощью двух хромель-копелевых термопар, включенных последовательно. Рабочие спаи термопар 5 помещаются в непосредственной близости к микропрессу. Термо-э.д.с. измеряется с помощью цифрового вольтметра 6.

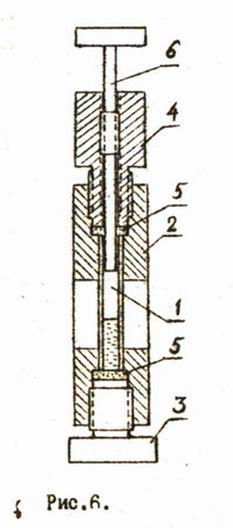
Устройство микропресса, совмещающего в себе конструктивно рабочую камеру и миниатюрный пресс, показано на рис.6. Рабочим объемом иикропресса является объём тонкой стеклянной трубки 1, которая помещается в корпус пресса 2. С обоих торцов стеклянная трубка герметически закрывается винтами 3 и 4 с фторопластовыми уплотнениями 5. Внутри винта 4 по резьбе может перемещаться поршень 6 и таким образом менять рабочий объём. Визуальное наблюдение за изменением состояния вещества производится через смотровые щели в корпусе пресса и в корпусе термостате.

III. ИЗМЕРЕНИИ. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ.

В процессе выполнения лабораторной работы необходимо провести градуировку термопар и построение градировочной кривой. Для этого предварительно включить вольтметр, а затем, через 20-30 минут, включить нагреватели термостата. Вместо микропрес-са в термостат помещается ртутный термометр с пределами измерения от 0°С до 350°С. В процессе повышения температуры необходимо записывать показания вольтметра и термометра через Dt=20°С. Затем надо включить нагрев термостата и записать соответствующие показания при остывании. Окончательные результаты градуировки представить в виде графика: по вертикали откладываются показания вольтметра в милливольтах U, по горизонтали разность между температурой термостата и комнатной температурой. Необходимо брать именно разность температур, поскольку "холодные" спаи термопар находятся при комнатной температуре.

После проведения градуировки заполнить микропресс исследуемым веществом со стороны винта 3 с помощью шприца. Поршень при этом должен быть введён в стеклянную, трубку до соответствующей отметки, примерно на 3/4 длины. Далее необходимо винтом 3 с уплотнением закрыть пресс так, чтобы в стеклянную трубку не попал пузырёк воздуха. Винты 3 и 4 надо крепко закрутить. После этого поршень можно вывести из стеклянной трубки таким образом, чтобы образовавшаяся при этом газообразная фаза занимала примерно такой же объём, как и жидкая. Затем пресс помещают в термостат так, чтобы рукоятка поршня находилась сверху за пределами термостата и включают нагрев.

В процессе нагревания необходимо следить за положением менискаи, перемещая поршень, в ту или другую сторону, не давать ему уйти из поля зрения. При определенной температуре мениск должен исчезнуть. Это критическая температура. Вещество в критическим состоянии интенсивно рассеивает свет и становится мутно-белым, непрозрачным. В данной установке детали микропресса выходят за пределы термостата, через них происходит интенсивный теплоотвод, Поэтому температура в стеклянной трубке неоднородна, и критическое состояние может быть получено только в нижней части трубки. Это и наблюдается в эксперименте. В верхней части трубки при этом может наблюдаться граница раздела двух фаз.

В процессе работы необходимо измерить температуру, при которой в нижней части стеклянной трубку начнется интенсивное рассеяние света веществом. Затем нагреватели необходимо выключить и измерить температуру, при которой это рассеяние исчезнет. Подобные измерения провести несколько рез и в качестве критической температуры взять среднее значение.

Таблица 1.

Вещество	Этиловый спирт	Диэтиловый эфир	Ацетон	Гексан	Изопропиловый спирт
Критическое давление атм.		35,6	46,6	29,9

По результатам измерения критической температуры. и используя данные таблицы 1 для критического давления, рассчитать константы Ван-дер-Ваальса 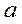и 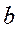для исследуемого вещества.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1) Для чего введены константы 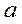и 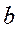в уравнение Ван-дер-Ваальса?

2) Сравнить систему реальных изотерм и систему изотерм Ван-дер-Ваальса.

3) Как меняется давление насыщения при изменении температуры?

4) Рассказать о двух методах вывода формул для критических параметров.

5) Написать приведенное уравнение Ван-дер-Ваальса.

6)
Сформулировать закон соответственных состояний.

ЛИТЕРАТУРА.

1) А.К.Кикоин, И.К.Кикоин. Молекулярная физика. Изд."Наука",1976, с.208-237.

2) Д.В.Сивухин. Общий курс физики. Т.П, изд."Наука", 1976,с.371-399.