2015-05-10
509
Апериодическое звено второго порядка. Уравнение и передаточная функция звена имеют вид
,
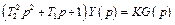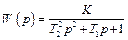
причем предполагается, что T 1 >= 2 T 2 так как при этом корни характеристического уравнения
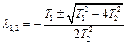
будут вещественными. Передаточную функцию апериодического звена второго порядка можно записать в виде
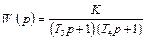
где
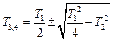
Амплитудная и фазовая частотные характеристики звена:
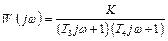
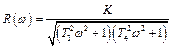
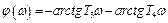
Логарифмическая амплитудная частотная характеристика звена:
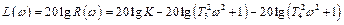
При T 1 < 2 T 2 звено переходит в колебательное (см. ниже) состояние, поэтому постоянная Т 1, определяющая инерционность звена, является в то же время демпфирующим фактором (увеличение Т 1 приводит к отсутствию колебаний). Переходная и весовая функции аналогично предыдущему имеют вид
,
.
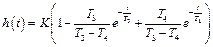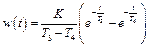Примерами такого звена являются: а) двигатель постоянного тока при учете инерционности цепи якоря; б) электромашинный усилитель; в) двойная LR -цепочка.
Колебательное звено. Уравнение и передаточная функция звена:
,
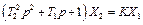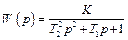
причем предполагается T 1<2 T 2, так что корни характеристического уравнения –
|
|
|
комплексные. Общепринята запись передаточной функции колебательного звена в виде
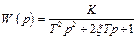
где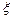 
= T 1/(2 T 2), причем 0 < 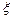< 1, так как при 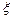= > 1 звено становится апериодическим второго порядка.
Передаточная функция колебательного звена имеет два комплексных полюса:
,
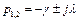где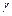 
- действительная, а 
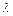- мнимая части полюсов передаточной функции.
Постоянная времени и коэффициент демпфирования колебательного звена связаны с действительной и мнимой частями полюсов передаточной функции формулами
; 
.
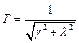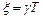Для экспериментального определения параметров колебательного звена можно использовать следующие свойства его переходной функции (рис.2.2).
– период колебаний переходной функции равен 2p/l, где l – мнимая часть полюсов передаточной функции;
– действительная часть полюсов передаточной функции g находится по формуле:
,
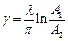где А1 и А2 – амплитуды соседних положительной и отрицательной полуволн колебаний переходной функции относительно установившегося значения;
– установившееся значение переходной функции равно коэффициенту передачи, т.к. сигнал на входе равен единице.
Данные утверждения поясняются на рис. 4.
Амплитудная и фазовая частотные характеристики звена:
,
.
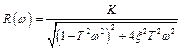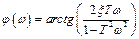Амплитудная характеристика уменьшается с увеличением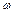 
, т.е. R (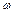) < K, если 1 > 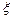> 0.707. При 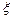<0.707 появляется "горб" на характеристике R (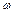), который уходит в бесконечность при 
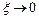. Поэтому величина
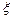= T 1/(2 T 2)
называется параметром затухания (демпфирования). Отсюда видна роль постоянных времени T 1 и Т 2 в уравнении звена: постоянная T 1 "раскачивает" колебания, а T 2 - "демпфирует" их.
|
|
|
Логарифмическая амплитудная частотная характеристика звена
.
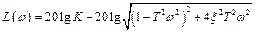Выражения переходной и весовой функций колебательного звена соответственно имеют вид
,
.
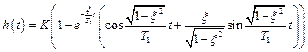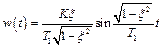Они имеют вид, показанный на рис. 4 и 5 соответственно.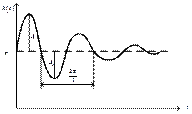 
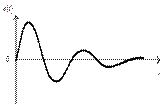
Рис. 4. Переходная функция Рис. 5. Функция веса
