Статистическая проверка адекватности модели

Все приведенные выше выражения справедливы при выполнении предположения о том, что истинный вид зависимости заранее известен, причем эта зависимость линейна по искомым параметрам. Если же это не так, что обычно и имеет место, то утверждение о несмещенности оценок 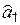, 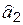параметров 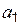, 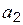оценки 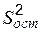дисперсии 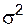и оценки 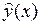(эмпирической зависимости) неизвестной истинной зависимости 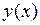становится необоснованным, и правильнее исходить из предположения об их смещенности. Для того, чтобы проверить гипотезу о несмещенности модели (говорят об адекватности модели опытным данным), пользуются статистическими критериями.

Известный F-критерий проверки адекватности модели опытным данным использует статистику в виде отношения остаточной дисперсии 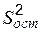(6.7) к независимой несмещенной оценке дисперсии опытных данных 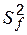, где 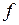– число степеней свободы этой оценки:

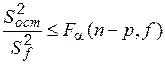. (6.9)

На практике исследователь часто не имеет в своем распоряжении независимой несмещенной оценки дисперсии опытных данных и не может воспользоваться критерием (6.9). В этом случае можно воспользоваться следующим критерием:

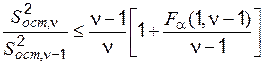. (6.10)

Этот критерий использует статистику в виде отношения двух последовательных по числу параметров модели остаточных дисперсий; здесь, как обычно, число степеней свободы 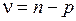. В нашем конкретном случае, когда модель имеет вид прямой линии, остаточная дисперсия (6.7) соответствует 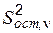(числитель статистики). Для нахождения знаменателя следует перейти к более сложной модели, содержащей не 2, а 3 параметра (параболе второй степени), и найти для нее остаточную дисперсию. Однако этот вопрос выходит за рамки изучаемого курса, поэтому в данной работе предполагается, что имеется независимая несмещенная оценка дисперсии, либо известна сама дисперсия .

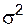Линейному регрессионному анализу посвящено множество работ разной сложности, из которых отметим [6, 12, 13, 14]. Наиболее доступно он изложен в [5, 6].