Цель работы
Изучить основные особенности и методы построения линейного приближения экспериментальных данных.
Задание
Методом наименьших квадратов построить линейную эмпирическую зависимость по опытным данным. Выполнить проверку адекватности математической модели опытным данным с помощью статистических критериев. Оценить погрешность эмпирической зависимости совместными доверительными F-интервалами.
Краткая теория
Метод наименьших квадратов
Одновременные измерения двух или более разнородных физических величин с целью нахождения зависимости между ними называются совместными измерениями [2]. Обычно выполняется 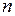 измерений, при которых в заданных или точно измеренных значениях аргумента
измерений, при которых в заданных или точно измеренных значениях аргумента 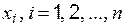
определены значения функции 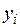 . Задача состоит в том, чтобы по
. Задача состоит в том, чтобы по 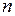 парам (
парам (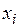 ,
, 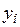 ) построить зависимость (эмпирическую), которая была бы несмещенной и эффективной оценкой истинной зависимости, общий вид которой считают известным. Например, известно, что истинная зависимость есть прямая линия, представленная в виде
) построить зависимость (эмпирическую), которая была бы несмещенной и эффективной оценкой истинной зависимости, общий вид которой считают известным. Например, известно, что истинная зависимость есть прямая линия, представленная в виде
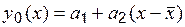 . (6.1)
. (6.1)
Параметры 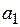 ,
, 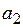 неизвестны, их следует оценить по опытным данным. Будем считать ошибки измерений
неизвестны, их следует оценить по опытным данным. Будем считать ошибки измерений 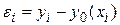 случайными с нулевым математическим ожиданием и дисперсией
случайными с нулевым математическим ожиданием и дисперсией 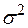 при любом
при любом 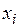 , а также некоррелированными для разных
, а также некоррелированными для разных 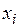 . При этих условиях найти несмещенные и эффективные оценки
. При этих условиях найти несмещенные и эффективные оценки 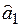 ,
, 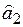 параметров
параметров 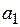 ,
, 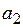 (а следовательно и зависимости (6.1) в целом) можно с помощью метода наименьших квадратов (МНК).
(а следовательно и зависимости (6.1) в целом) можно с помощью метода наименьших квадратов (МНК).
Будем определять оценку 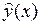 функции
функции 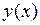 в виде
в виде
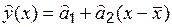 , (6.2)
, (6.2)
а оценки 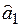 ,
, 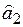 искать таким способом, чтобы сумма квадратов отклонений
искать таким способом, чтобы сумма квадратов отклонений 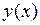 от
от 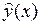 по всем узлам была минимальной (этот подход называют также принципом Лежандра):
по всем узлам была минимальной (этот подход называют также принципом Лежандра):
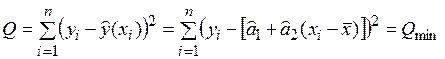 . (6.3)
. (6.3)
Это эквивалентно условию 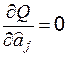 , что приводит к уравнениям вида:
, что приводит к уравнениям вида:
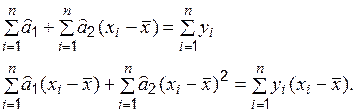 (6.4)
(6.4)
Учитывая, что 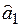 ,
, 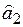 – некоторые числа, при этом
– некоторые числа, при этом 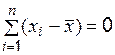 , получаем
, получаем
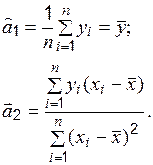 (6.5)
(6.5)
Отметим, что если бы мы записали выражение (6.1) в обычном виде 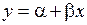 , мы вынуждены были бы решать систему уравнений, выражая параметры один через другой и проводя более сложные вычисления. Использование линейной зависимости в виде (6.1) позволило упростить вычисления (что очень важно для более сложных зависимостей) и получить статистически независимые оценки
, мы вынуждены были бы решать систему уравнений, выражая параметры один через другой и проводя более сложные вычисления. Использование линейной зависимости в виде (6.1) позволило упростить вычисления (что очень важно для более сложных зависимостей) и получить статистически независимые оценки 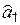 и
и 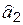 .
.
Учитывая это свойство, можно записать:
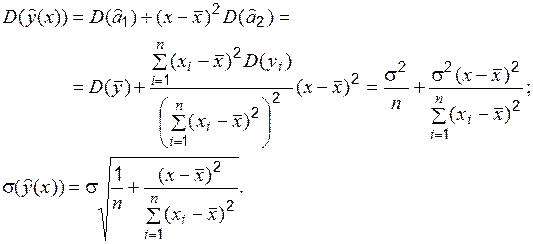
Переходя к оценкам, получаем:
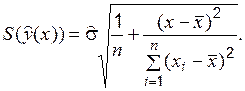 (6.6)
(6.6)
При любом законе распределения (если удовлетворяются указанные выше условия) несмещенной оценкой 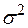 (а при нормальном законе распределения и эффективной) является остаточная дисперсия
(а при нормальном законе распределения и эффективной) является остаточная дисперсия
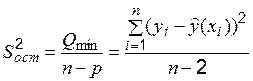 , (6.7)
, (6.7)
где 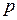 – число коэффициентов регрессии (для прямой линии
– число коэффициентов регрессии (для прямой линии 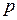 =2).
=2).
Окончательно получаем
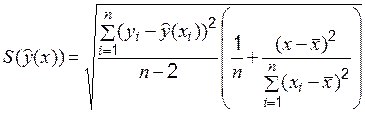 , (6.8)
, (6.8)
то есть оценка СКО 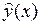 является функцией от
является функцией от 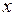 . Значение
. Значение 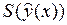
минимально при 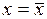 и увеличивается к началу и к концу интервала значений аргумента.
и увеличивается к началу и к концу интервала значений аргумента.
 2015-05-10
2015-05-10 442
442







