Рассмотри уравнение регрессии вида:
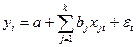 (1)
(1)
где 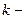 число независимых переменных модели.
число независимых переменных модели.
Наиболее известным критерием обнаружения автокорреляции в случае модели (1) является критерий Дарбина-Уотсона. Для анализа коррелированности отклонений вместо коэффициента корреляции 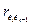 используют тесно с ним связанную статистику Дарбина-Уотсона DW, рассчитываемую по формуле:
используют тесно с ним связанную статистику Дарбина-Уотсона DW, рассчитываемую по формуле: 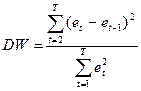 .
.
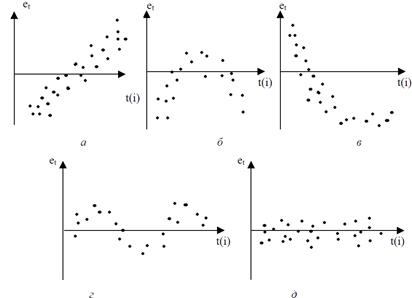
Рис. 3.
Общая схема критерия Дарбина–Уотсона для выявления автокорреляции остатков.
1. Выдвинуть гипотезы: нулевую гипотезу 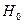 об отсутствии автокорреляция и гипотезы
об отсутствии автокорреляция и гипотезы 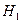 и
и 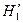 соответственно о наличии положительной и отрицательной автокорреляции в остатках.
соответственно о наличии положительной и отрицательной автокорреляции в остатках.
2. Построить уравнение регрессии и определить значения остатков 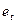 для каждого наблюдения
для каждого наблюдения 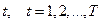 .
.
3. По формуле 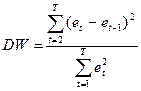 вычислить значение статистики
вычислить значение статистики 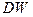 .
.
4. По таблице критических точек Дарбина-Уотсона определить значения критерия Дарбина-Уотсона 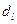 (нижнее) и
(нижнее) и 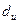 (верхнее) для заданного числа наблюдений
(верхнее) для заданного числа наблюдений 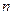 , числа независимых переменных модели
, числа независимых переменных модели 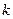 и уровня значимости
и уровня значимости 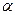 . По этим значениям числовой промежуток
. По этим значениям числовой промежуток 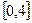 разбивают на пять отрезков:
разбивают на пять отрезков: 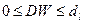 ,
, 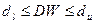 ,
, 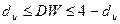 ,
, 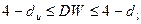 и
и 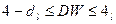 .
.
5. Сделать вывод о наличии (или отсутствии автокорреляции) по правилу:
a. если 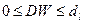 , то существует положительная автокорреляция; гипотеза
, то существует положительная автокорреляция; гипотеза 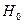 отклоняется и с вероятностью
отклоняется и с вероятностью 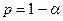 принимается гипотеза
принимается гипотеза 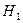 ;
;
b. если 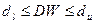 , то попадаем в так называемую зону неопределенности и не имеем возможности ни опровергнуть, ни принять ни одну из гипотез.
, то попадаем в так называемую зону неопределенности и не имеем возможности ни опровергнуть, ни принять ни одну из гипотез.
c. если 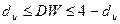 , то нет оснований отклонить нулевую гипотезу: автокорреляция отсутствует;
, то нет оснований отклонить нулевую гипотезу: автокорреляция отсутствует;
d. если 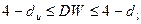 , то попадаем в так называемую зону неопределенности и не имеем возможности ни опровергнуть, ни принять ни одну из гипотез.
, то попадаем в так называемую зону неопределенности и не имеем возможности ни опровергнуть, ни принять ни одну из гипотез.
e. если 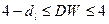 , то существует отрицательная автокорреляция: гипотеза
, то существует отрицательная автокорреляция: гипотеза 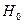 отклоняется и с вероятностью
отклоняется и с вероятностью 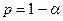 принимается гипотеза
принимается гипотеза 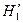 .
.
Ограничения на применение критерия Дарбина–Уотсона:
- неприменим к моделям с лаговыми переменными;
- выявляет автокорреляции только первого порядка;
- дает достоверные результаты только для больших выборок;
- применяется только для тех моделей, которые содержат свободный член.
На практике если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то предполагают существование автокорреляции остатков и отклоняют нулевую гипотезу. В ряде случаев устранить автокорреляцию можно путем определения ответственного за нее фактора или факторов и соответствующего расширения уравнения регрессии. Можно также изменить формулу зависимости между факторами.
ПОСТАНОВКА ЗАДАЧИ
Для статистических данных, представленных в таблице согласно вашему варианту, проверьте наличие автокорреляции на уровне значимости 0,05, используя критерий Дарбина – Уотсона. Сделайте вывод о пригодности полученного уравнения регрессии для построения прогнозов.
1. В главном меню выберите последовательно пункты: Сервис – Анализ данных – Регрессия
2. Заполните диалоговое окно инструмента Пакета анализа Регрессия
Входные данные:
Входной интервал 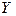 – диапазон (столбец или строка), содержащий данные результативного признака. – Необходимо выделить столбец с признаком
– диапазон (столбец или строка), содержащий данные результативного признака. – Необходимо выделить столбец с признаком 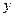 .
.
Входной интервал 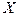 – диапазон, содержащий данные факторов независимых признаков (одновременно выделяются столбцы, содержащие значения факторных признаков
– диапазон, содержащий данные факторов независимых признаков (одновременно выделяются столбцы, содержащие значения факторных признаков 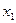 и
и 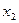 )
)
Метки (да или нет) – флажок, который указывает, содержит ли первая строка названия столбцов или нет.
Введите название листа, в котором будут выведены результаты расчета, заполнив поле Новый рабочий лист.
Поставьте флажок Остатки
3. Нажмите ОК. На отдельном листе появятся итогирегрессионного анализа, содержащие 4 таблицы:
Регрессионная статистика
Таблица без названия
Вывод остатка
4. Из Таблицы без названия выпишите значения коэффициентов уравнения регрессии и запишите само уравнение.
5. Из таблицы Вывод остатка скопируйте два столбца «Предсказанное 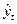 » и «Остатки
» и «Остатки 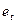 » и добавьте их в исходную таблицу данных.
» и добавьте их в исходную таблицу данных.
6. Дополните таблицу данных столбцами «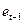 », «Квадрат разности остатков
», «Квадрат разности остатков 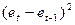 » и «Квадрат остатка
» и «Квадрат остатка 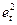 ».
».
7. Используя процедуру Автосумма, вычислите нужные суммы 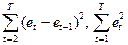 .
.
В результате выполнения пп.1 - 3 получаем таблицу:
| № | 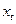 | 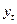 | Предсказанное 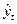 | Остатки 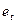 | 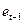 | 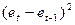 | 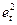 |
| - | - | ||||||
| … | |||||||
| Сумма: |
8. По формуле 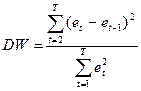 вычислите значение статистики
вычислите значение статистики 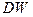 .
.
9. По таблице критических точек Дарбина-Уотсона определите значения критерия Дарбина-Уотсона 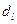 (нижнее) и
(нижнее) и 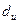 (верхнее) для заданного числа наблюдений
(верхнее) для заданного числа наблюдений 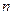 , числа независимых переменных модели
, числа независимых переменных модели 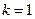 и уровня значимости
и уровня значимости 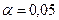 .
.
10. По этим значениям числовой промежуток 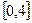 разбейте на пять отрезков:
разбейте на пять отрезков:
· – 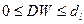 ,
,
· – 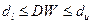 ,
,
· – 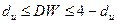 ,
,
· – 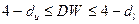 ,
,
· – 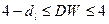 .
.
11. Определите, какому отрезку принадлежит найденное значение 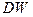 и сделайте вывод.
и сделайте вывод.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем заключается суть автокорреляции? Положительная и отрицательная автокорреляция.
2. Причины возникновения автокорреляции.
3. Последствия автокорреляции.
4. Графический метод обнаружения автокорреляции.
5. Тест Дарбина-Уотсона.
Вариант №1
| Месяц | Товарооборот, % к предыдущему месяцу, Х | Доходы населения, % к предыдущему месяцу, У |
| Январь | 91,5 | 79,5 |
| Февраль | 92,8 | 100,3 |
| Март | 104,3 | 102,9 |
| Апрель | 101,5 | 106,6 |
| Май | 97,9 | 92,5 |
| Июнь | 98,7 | 110,1 |
| Июль | 100,8 | 96,6 |
| Август | 103,7 | 97,1 |
| Сентябрь | 104,6 | 98,5 |
| Октябрь | 100,3 | 105,7 |
| Ноябрь | 101,5 | 97,4 |
| Декабрь | 116,0 | 129,9 |
| Январь | 82,3 | 63,9 |
| Февраль | 91,6 | 104,3 |
| Март | 103,4 | 101,7 |
Вариант №2
| месяц | Оборот розничной торговли, % к предыдущему месяцу, Х | Индекс потребительских цен, % к предыдущему месяцу, У |
| Октябрь | 102,3 | 99,8 |
| Ноябрь | 102,9 | 102,7 |
| Декабрь | 123,1 | 109,4 |
| Январь | 74,3 | 110,0 |
| Февраль | 92,9 | 106,4 |
| Март | 106,0 | 103,2 |
| Апрель | 99,8 | 103,2 |
| Май | 105,2 | 102,9 |
| Июнь | 99,7 | 100,8 |
| Июль | 99,7 | 101,6 |
| Август | 107,9 | 101,5 |
| Сентябрь | 98,8 | 101,4 |
| Октябрь | 104,6 | 101,7 |
| Ноябрь | 106,4 | 101,7 |
| Декабрь | 122,7 | 101,2 |
Вариант №3
| № | Х, у.е. | Y,у.е. |
| 7,0 | 7,3 | |
| 7,3 | 7,6 | |
| 7,8 | 8,3 | |
| 8,3 | 8,9 | |
| 8,6 | 9,5 | |
| 8,9 | 10,0 | |
| 9,6 | 10,7 | |
| 9,6 | 10,8 | |
| 10,3 | 11,3 | |
| 10,9 | 11,9 | |
| 11,2 | 12,1 | |
| 11,4 | 12,2 | |
| 11,5 | 13,1 | |
| 11,8 | 13,5 | |
| 12,2 | 13,9 | |
| 12.3 | 14,0 |
 2015-05-10
2015-05-10 864
864







