Проверка гипотез о законе распределения

Статистический анализ характеристик объекта

1. Цель работы: провести статистический анализ характеристик объекта, определив его закон распределения, изучив критерии согласия, такие как критерий Пирсона, Колмагорова, Шапиро-Уилка.

Теоретические положения

Проверка гипотез о законе распределения

Во многих случаях закон распределения изучаемой случайной величины неизвестен, но есть основания предположить, что он имеет вполне определенный вид: нормальный, биномиальный или какой – либо другой.

Пусть необходимо проверить гипотезу 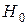о том, что свободная величина 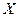подчиняется определенному закону распределения, заданному функцией распределения 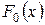, т.е. 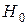: 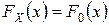. Под альтернативной гипотезой 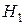будем понимать в данном случае то, что просто не выполнена основная (т.е. : ).

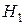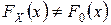Для проверки гипотезы о распределении случайной величины 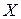проведем выборку, которую оформим в виде статистического ряда:

			…
			…

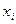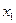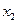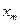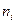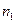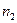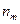где 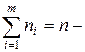объем выборки.

Требуется сделать заключение: согласуется ли результаты наблюдений с высказанным предположением. Для этого используем специально подобранную величину – критерий согласия.

Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения. (Он используется для проверки согласия предполагаемого вида распределения с опытными данными на основании выборки).

Существуют различные критерии согласия: Пирсона, Колмогорова, Фишера, Смирнова и др.

Критерий согласия Пирсона – наиболее часто употребляемый критерий для проверки простой гипотезы о законе распределения.

2.1.1. Критерий 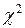Пирсона

Для проверки гипотезы 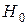поступают следующим образом.

Разбивают всю область значений случайной величины 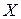на 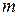интервалов 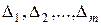и подсчитывают вероятности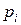 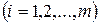попадания случайной величины 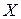(т.е. наблюдения) в интервал 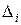, используя формулу:

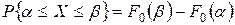
Тогда теоретическое число значений случайной величины 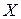, попавших в интервал 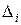можно рассчитать по формуле 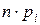. Таким образом, имеем статистический ряд распределения случайной величины :

			…
			…

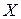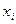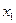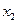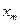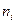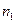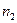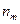и теоретический ряд распределения:

		…
		…

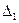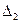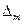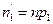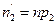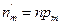Если эмпирические частоты 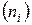сильно отличаются от теоретических 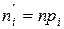, то проверяемую гипотезу 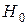следует отвергнуть; в противном случае – принять.

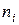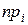Каким критерием, характеризующим степень расхождения между эмпирическими и теоретическими частотами, следует воспользоваться? В качестве меры расхождения между и для 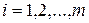К.Пирсон (1857 – 1936; англ. математик, статистик, биолог, философ) предложил величину («критерий Пирсона»):

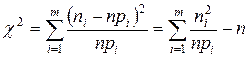
Согласно теореме Пирсона, при 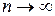статистика имеет 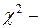распределение с 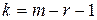степенями свободы, где 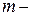число групп (интервалов) выборки, 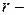число параметров предполагаемого распределения. В частности, если предполагаемое распределение нормально, то оценивают два параметра ( 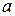и 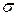), поэтому число степеней свободы .

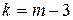Правило применения критерия 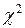сводится к следующему:

По формуле вычисляют 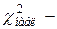выборочное значение статистики критерия.

Выбрав уровень значимости 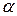критерия, по таблице 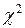- распределения находим критическую точку (квантиль) .

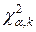Если 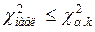, то гипотеза 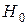не противоречит опытным данным: если 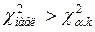, то гипотеза 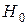отвергается.

Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений (т.е. 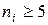). Если в отдельных интервалах их меньше, то число интервалов надо уменьшить путем объединения (укрупнения) соседних интервалов.