1. Вычислить производные в заданных точках:
| а) | б) | |
| 1. | 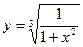 , х= 0, х =5 , х= 0, х =5
| 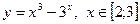 с шагом 0,1 с шагом 0,1
|
| 2. | 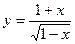 , х =-3, х =0 , х =-3, х =0
| 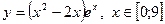 с шагом 1 с шагом 1
|
| 3. | 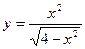 , х =1, х =-1 , х =1, х =-1
| 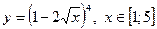 с шагом 0,5 с шагом 0,5
|
| 4. | 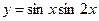 , х =0, х = , х =0, х = 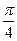
| 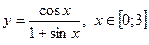 с шагом 0,4 с шагом 0,4
|
| 5. | 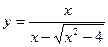 , х =-5, х =7 , х =-5, х =7
| 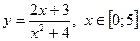 с шагом 0,5 с шагом 0,5
|
| 6. | 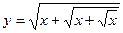 , х =0, х =3 , х =0, х =3
| 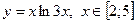 с шагом 0,3 с шагом 0,3
|
| 7. | 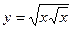 , х =1, х =4 , х =1, х =4
| 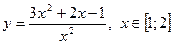 с шагом 0,1 с шагом 0,1
|
| 8. | 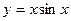 , х =0, х = , х =0, х = 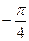
| 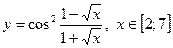 с шагом 0,5 с шагом 0,5
|
| 9. | 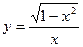 , х =0,1, х =1 , х =0,1, х =1
| 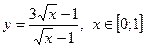 с шагом 0,2 с шагом 0,2
|
| 10. | 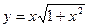 , х =-2, х =0,5 , х =-2, х =0,5
| 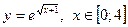 с шагом 0,5 с шагом 0,5
|
| 11. | 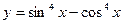 , х =0, х = , х =0, х = 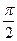
| 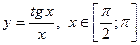 с шагом с шагом 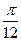
|
| 12. | 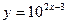 , х =5, х =0,1 , х =5, х =0,1
| 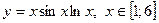 с шагом 0,5 с шагом 0,5
|
| 13. | 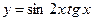 , х = , х = 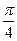 , х = , х = 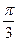
| 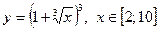 с шагом 0,8 с шагом 0,8
|
| 14. | 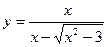 , х =5, х =5,6 , х =5, х =5,6
| 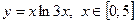 с шагом 0,4 с шагом 0,4
|
| 15. | 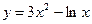 , х =1, х =2 , х =1, х =2
| 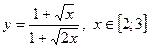 с шагом 0,1 с шагом 0,1
|
| 16. | 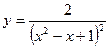 , х =5, х =0,5 , х =5, х =0,5
| 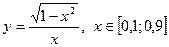 с шагом 0,1 с шагом 0,1
|
| 17. | 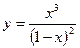 , х =3, х =0,3 , х =3, х =0,3
| 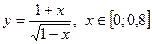 с шагом 0,1 с шагом 0,1
|
| 18. | 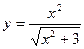 , х =0,5, х =3 , х =0,5, х =3
| 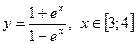 с шагом 0,1 с шагом 0,1
|
| 19. | 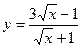 , х =1, х =2,5 , х =1, х =2,5
| 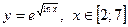 с шагом 0,5 с шагом 0,5
|
| 20. | 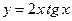 , х =0, х = , х =0, х = 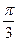
| 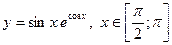 с шагом с шагом 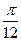
|
2. Найти производные от заданных функций:
| а) | б) | |
| 1. | 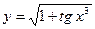
| 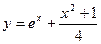
|
| 2. | 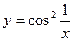
| 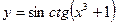
|
| 3. | 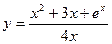
| 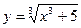
|
| 4. | 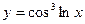
| 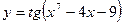
|
| 5. | 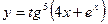
| 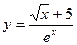
|
| 6. | 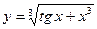
| 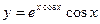
|
| 7. | 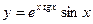
| 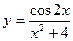
|
| 8. | 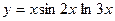
| 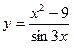
|
| 9. | 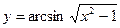
| 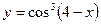
|
| 10. | 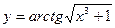
| 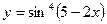
|
| 11. | 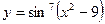
| 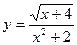
|
| 12. | 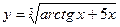
| 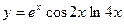
|
| 13. | 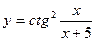
| 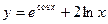
|
| 14. | 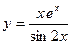
| 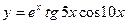
|
| 15. | 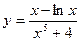
| 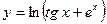
|
| 16. | 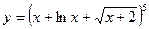
| 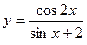
|
| 17. | 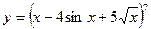
| 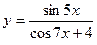
|
| 18. | 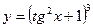
| 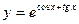
|
| 19. | 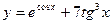
| 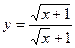
|
| 20. | 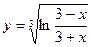
| 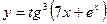
|
3. Найти значения указанных производных в заданных точках:
| а) | б) | |
| 1. | 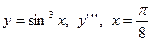
| 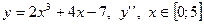 с шагом 0,5 с шагом 0,5
|
| 2. | 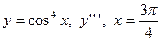
| 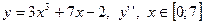 с шагом 0,7 с шагом 0,7
|
| 3. | 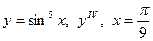
| 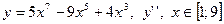 с шагом 0,6 с шагом 0,6
|
| 4. | 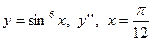
| 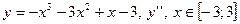 с шагом 0,5
с шагом 0,5
|
| 5. | 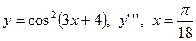
| 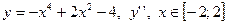 с шагом 0,4 с шагом 0,4
|
| 6. | 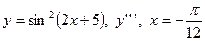
| 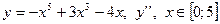 с шагом 0,5 с шагом 0,5
|
| 7. | 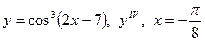
| 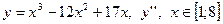 с шагом 0,7 с шагом 0,7
|
| 8. | 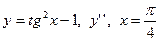
| 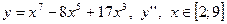 с шагом 0,7 с шагом 0,7
|
| 9. | 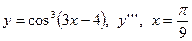
| 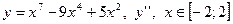 с шагом 0,3 с шагом 0,3
|
| 10. | 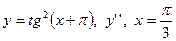
| 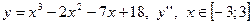 с шагом 0,3
с шагом 0,3
|
| 11. | 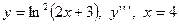
| 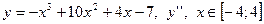 с шагом 0,4
с шагом 0,4
|
| 12. | 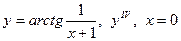
| 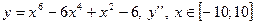 с шагом 2
с шагом 2
|
| 13. | 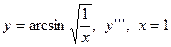
| 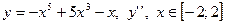 с шагом 0,4 с шагом 0,4
|
| 14. | 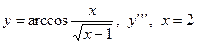
| 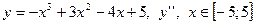 с шагом 1
с шагом 1
|
| 15. | 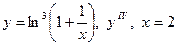
| 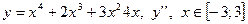 с шагом 0,3
с шагом 0,3
|
| 16. | 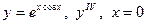
| 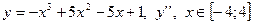 с шагом 0,4
с шагом 0,4
|
| 17. | 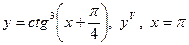
| 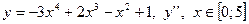 с шагом 0,5
с шагом 0,5
|
| 18. | 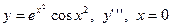
| 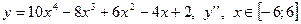 с шагом 1
с шагом 1
|
| 19. | 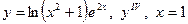
| 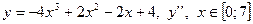 с шагом 0,5
с шагом 0,5
|
| 20. | 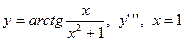
| 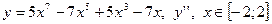 с шагом 0,4
с шагом 0,4
|
4. Найти указанные производные:
| а) | б) | |
| 1. | 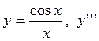
| 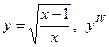
|
| 2. | 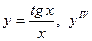
| 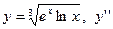
|
| 3. | 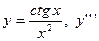
| 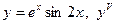
|
| 4. | 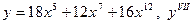
| 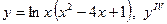
|
| 5. | 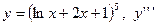
| 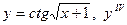
|
| 6. | 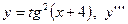
| 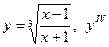
|
| 7. | 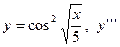
| 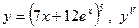
|
| 8. | 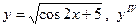
| 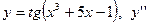
|
| 9. | 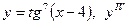
| 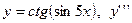
|
| 10. | 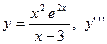
| 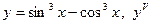
|
| 11. | 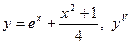
| 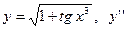
|
| 12. | 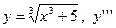
| 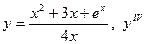
|
| 13. | 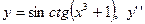
| 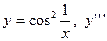
|
| 14. | 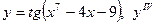
| 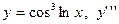
|
| 15. | 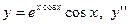
| 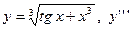
|
| 16. | 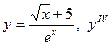
| 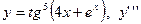
|
| 17. | 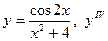
| 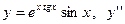
|
| 18. | 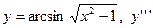
| 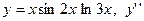
|
| 19. | 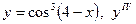
| 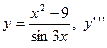
|
| 20. | 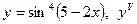
| 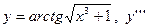
|
5*. Найти производные первого и второго порядков от функций, заданных параметрически.
Для нахождения производных использовать формулы: 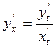 ,
, 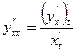 .
.
1. 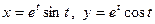 ;
;
2. 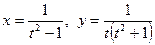 ;
;
3. 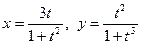 ;
;
4. 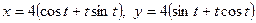 ;
;
5. 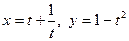 ;
;
6. 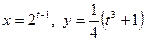 ;
;
7. 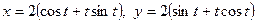 ;
;
8. 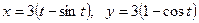 ;
;
9. 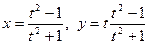 ;
;
10. 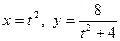 ;
;
11. 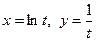 ;
;
12. 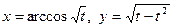 ;
;
13. 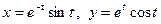 ;
;
14. 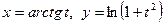 ;
;
15. 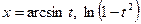 ;
;
16. 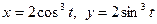 ;
;
17. 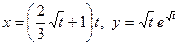 ;
;
18. 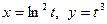 ;
;
19. 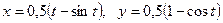 ;
;
20. 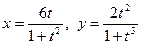 .
.
СПИСОК ЛИТЕРАТУРЫ
1. Банах С. Дифференциальное и интегральное исчисление. – М.: Наука, 1972.
2. Выгодский М.Я. Справочник по высшей математике. – М., 2002.
3. Гусак Г.М. Системы алгебраических уравнений. – Минск, 1983.
4. Давыдов Н.А. Сборник задач по математическому анализу. – М: Просвещение, 1973.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.2. – М.: Высшая школа, 1986.
6. Ефимов А.В. и др. Сборник задач по математике для втузов. Специальные разделы математического анализа. Ч.2. – М.: Наука, 1991.
7. Кудрявцев Е.М. MathCAD 2000 Pro. – М., 2001.
8. Фролов С.В., Шостак Р.Я. Курс высшей математики. – М., 1973.
9. Херкагер М., Партолль Х. MathCAD 2000. Полное руководство. – Киев: Ирина, BHV, 2000.
 2015-05-10
2015-05-10 390
390







