Краткие теоретические сведения. Если к концам проводника с омическим сопротивлением приложена ЭДС, значение которой в каждый момент времени определяется уравнением

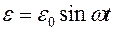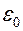Если к концам проводника с омическим сопротивлением приложена ЭДС, значение которой в каждый момент времени определяется уравнением , где − амплитуда; 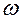− круговая частота, то в нём возникает переменный электрический ток, сила которого в данный момент времени определяется по закону Ома:

(17.1)

В этом случае ток и напряжение совпадают по фазе.

Если в цепи есть ещё и катушка индуктивности, характеризуемая индуктивностью L и сопротивлением X_L, то под действием той же ЭДС возникает ток:

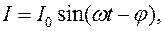(17.2)

где амплитудная сила тока

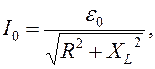(17.3)

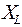− индуктивное сопротивление

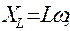(17.4)

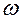− круговая частота, 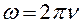; n − линейная частота.

В этом случае ток отстаёт по фазе от напряжения на угол j:

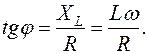(17.5)

Если вместо катушки в цепь ввести конденсатор ёмкостью С, то под действием той же ЭДС в цепи возникает ток

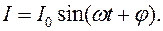(17.6)

При этом амплитудная сила тока

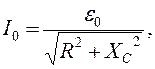(17.7)

где 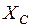− ёмкостное сопротивление

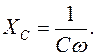(17.8)

В этом случае ток опережает напряжение на j:

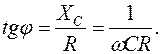(17.9)

Если цепь состоит из последовательно включенных нагрузок: активной, ёмкостной и индуктивной, то в цепи под действием той же ЭДС возникает ток

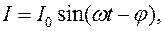(17.10)

где 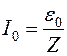или

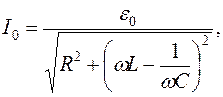(17.11)

где полное сопротивление

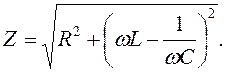(17.12)

Формула (17.11) выражает закон Ома для последовательной цепи переменного тока. При этом угол сдвига фаз между током и напряжением

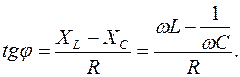(17.13)

В приведенных формулах I ₀ и e ₀ − максимальные (амплитудные) токи и напряжения. Приборы показывают эффективные значения, которые в 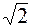раз меньше максимальных, т.е.

, , .

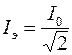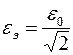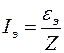Преобразуем формулу следующим образом:

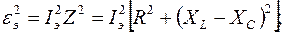
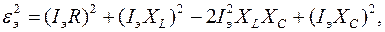
или

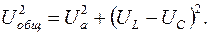(17.14)