Дисперсия числа появлений события в независимых испытаниях

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна. Чему равна дисперсия числа появлений события в этих испытаниях? Ответ на этот вопрос дает следующая теорема.

Теорема. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D (X) = npq.

Замечание. Так как величина X распределена по биномиальному закону, то доказанную теорему можно сформулировать и так: дисперсия биномиального распределения с параметрами n и р равна произведению npq.

Пример. Производятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X — числа появлений события в этих испытаниях.

Решение. По условию, n=10, р = 0,6. Очевидно, вероятность непоявления события

q= 1–0,6 = 0,4.

Искомая дисперсия D (X) = npq= 10*0,6*0,4 = 2,4.

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики.

1) Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии: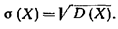

2) Среднее квадратическое отклонение суммы взаимно независимых случайных величин

3) Одинаково распределенные взаимно независимые случайные величины

4) Начальные и центральные теоретические моменты/

Эти характеристики могут использоваться при решении различных задач.

В теории случайных процессов используются теорема Чебышева и теорема Брнулли, рассматриваются различные виды распределения случайных величин.