2015-05-12
1005
Теперь выпишем пути, которые начинаются с ребра АВ (также сверху вниз):
АВДИК, АВДК, АВЖК
и, наконец, пути, начинающиеся с участка АГ:
АГВДИК, АГВДК, АГВЖК, АГЕЖК, АГЕК.
Всего получилось 13 путей. Это наиболее простой метод, но он нередко приводит к неправильному результату, потому что легко пропустить какойто путь.
Способ 2. Пошаговое построение всех возможных путей.
Сначала рассмотрим все вершины, куда можно попасть из начальной вершины А за один шаг:
АБ
АВ
АГ
Теперь выписываем все пути из вершины A, содержащие два ребра (продолжения уже построенных путей на одно ребро):
АБД АБВ
АВД АВЖ
АГВ АГЕ
Следующий шаг (в рамку обведены пути, дошедшие до конечного пункта K):
АБДИ АБДК АБВД АБВЖ
АВДИ АВДК АВЖК
АГВД АГВЖ АГЕЖ АГЕК
Итак, четыре пути из А в К мы уже нашли. Продолжая движение по остальным маршрутам, находим семь путей, состоящих из четырех ребер:
АБДИК АБВДИ АБВДК АБВЖК
АВДИК
АГВДИ АВГДК АГВЖК АГЕЖК
и далее два пути из пяти ребер:
АБВДИК
АГВДИК
Таким образом, всего найдено 4 + 7 + 2 = 13 путей, причем по построению других путей нет (в списке не осталось путей, не доведенных до конечной точки).
Этот способ более надежен, чем предыдущий, поскольку на каждом шаге нас интересуют только ребра, исходящие из одной вершины. Это значит, что нужно анализировать не весь граф, а только его небольшую часть, поэтому труднее ошибиться.
Задачи для тренировки
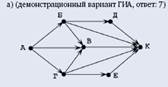
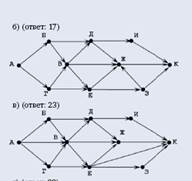
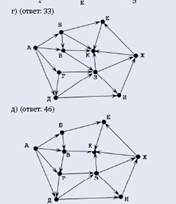На рисунке показана схема дорог. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
