Описание графа

Итак, граф — это (непустое) множество вершин и множество соединяющих их ребер. Эта структура естественно появляется тогда, когда в задаче есть несколько однотипных объектов и каждый из них может быть связан с произвольным количеством других объектов. В качестве объектов могут быть железнодорожные станции, маршрутизаторы локальных и глобальных сетей и т.п. В первом случае ребра графа — это дороги между станциями, во втором — каналы связи (кабельные, оптоволоконные, спутниковые и т.д.).

Для человека наиболее естественно использовать изображения графов (рисунки, схемы) для объяснения связей между элементами какой-то системы. Поскольку информатика занимается автоматической обработкой данных с помощью компьютеров, сразу возникает вопрос: “Как представить информацию о графе в памяти компьютера?” Хранить ее в виде рисунка (растрового или векторного) неэффективно, потому что рисунок предназначен для восприятия человеком, а не компьютером.

Компьютеру удобнее всего хранить информацию в виде таблиц (массив тоже можно считать простейшей таблицей). Для описания графа часто используют квадратную таблицу, которая описывает все возможные связи между узлами (без учета дублирования). Если, например, на пересечении строки A и столбца B записано число 1, это означает, что есть ребро, соединяющее вершины A и B; число 0 в этой ячейке означает, что такого ребра нет. Такую таблицу называют матрицей смежности. На рисунке показанаи схема дорог, соответствующий ей

граф и его матрица смежности:

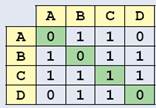
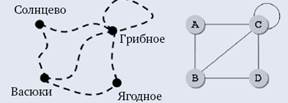
Единица на главной диагонали (выделенной серым цветом) показывает, что в графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.

Обратите внимание, что матрица смежности симметрична относительно главной диагонали, то есть если существует ребро из вершины A в вершину B, то существует и ребро из B в A. Такой граф называют неориентированным — ребра не имеют направления и каждое из них учтено в матрице смежности дважды.

Во многих практических задачах (например, при определении кратчайшего пути из одной вершины в другую) важную роль играет не только наличие связей между вершинами, но и “длины” этих связей, которые в теории графов называют “весами” (от слова “вес”). Весом может быть, например, длина дороги или стоимость авиаперелета. В этом случае вместо матрицы смежности используют весовую матрицу, в клетках которой записывают веса ребер, а если ребра нет, то клетку оставляют пустой. На рисунке показана схема, на которой указаны длины дорог, соответствующий ей граф и его весовая матрица:

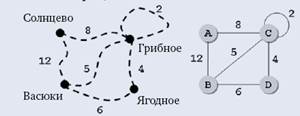
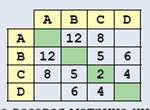
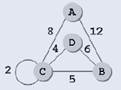
Заметим, что весовая матрица никак не определяет взаимное расположение вершин. Например, рассмотренный выше граф можно нарисовать совсем иначе, например, так:

Однако с точки зрения теории графов это будет тот же самый граф, поскольку весовая матрица не изменилась. По аналогии можно вспомнить, что в математике записи 0,5, 1/2, 3/6 и 5/10 обозначают одно и то же число.

Что можно выяснить с помощью весовой матрицы? Во-первых, определить, есть ли ребро между двумя заданными вершинами, и если есть, какова его длина (вес). Для этого достаточно посмотреть в соответствующую ячейку. Например, значение, выделенное кружком на рисунке, показывает, что между вершинами B и C есть ребро с весом 5:

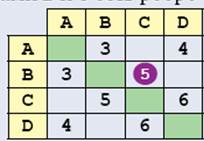Предполагая, что веса ребер обозначают расстояния между вершинами, можно определить длину пути, проходящего через заданные вершины, — сумму длин ребер, составляющих этот путь. В данном случае длина замкнутого пути ABCDA складывается из длин ребер AB, BC, CD и DA, которые определяются по таблице. Получаем: 3 + 5 + 6 + 4 = 18.

Наконец, полезно научиться рисовать граф по заданной весовой матрице. Нужно только помнить, что это можно сделать разными способами.

Для последней приведенной матрицы рисунок может быть, например, таким:

Вопросы и задачи:

1) Как по весовой матрице графа определить количество ребер (количество петель)?

2) Как можно обозначить отсутствие связи между вершинами при хранении весовой матрицы в памяти реального компьютера (рассмотрите разные варианты)?

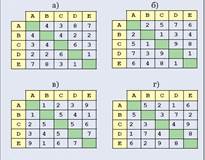3) Для каждой приведенной ниже весовой матрицы:

· определите вес ребра между вершинами B и D (если оно есть);

· предполагая, что веса ребер обозначают расстояния между вершинами, определите длину пути ABDCEA;

· укажите, какой из трех путей — ABDC, ADEC или AEBC — самый короткий, а какой самый длинный: