Определение простых форм высшей категории

Таблица 4

№ п/п	Названия простых форм	Кол-во граней	Форма граней
	Тетраэдр,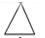
	тригонтритетраэдр
	Тетрагонтритетраэдр
	Пентагонтритетраэдр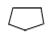
	Тригонгексатетраэдр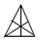
	Гексаэдр
	Тригонтетрагексаэдр
	Октаэдр
	Тригонтриоктаэдр	24
	Тетрагонтриоктаэдр
	Пентагонтриоктаэдр
	Тригонгексаоктаэдр
	Ромбододекаэдр
	Пентагондодекаэдр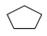
	Дидодекаэдр

Примечание. Все формы замкнутые.

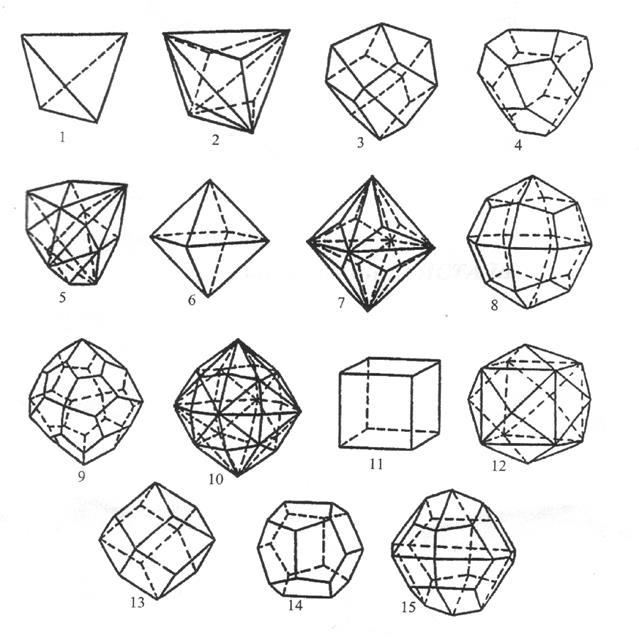
Рис.3. Простые формы кристаллов высшей категории:

1–тетраэдр; 2–тригонтритетраэдр; 3–тетрагонтритетраэдр;

4–пентагонтритетраэдр; 5–гексатетраэдр; 6–октаэдр; 7–тригонтриоктаэдр;

8–тетрагонтриоктаэдр; 9–пентагонтриоктаэдр; 10–гексагоноктаэдр;

11–гексаэдр; 12–тетрагексаэдр; 13–ромбододекаэдр; 14–пентагондодекаэдр;

15–дидодекаэдр

1.5. Установка кристаллов

Установка кристалла - это выбор координатных или кристаллографических осей. В отличие от кристаллофизической системы координат, которая является прямоугольной, кристаллографическая система в общем виде является косоугольной, а в тригональной и гексагональной сингонии принята даже четырехосная система (табл. 4).

Существует 2 теоремы:

1.Оси симметрии L_2, L_3, L_4, L_6, Li_4, L_i6; совпадают с рядами пространственной решётки и, следовательно, являются действительными или возможными рёбрами кристалла.

Следствие из теоремы 1: Кристаллографические оси можно совмещать с осями симметрии, т.к. они являются действительными или возможными рёбрами кристалла. Ребро многогранника - это ряд пространственной решётки.

2.Нормали к плоскостям симметрии совпадают с рядами пространственной решётки и, следовательно, являются действительными или возможными рёбрами кристалла.

Следствие из теоремы 2: Кристаллографические оси можно совмещать с нормалями к плоскостям симметрии, т.к. они являются действительными или возможными рёбрами кристалла.

При установке кристаллов следует руководствоваться следующими условиями:

· координатные оси можно совмещать с осями симметрии L_2, L_3, L_4, L_6, Li_4, L_i6;

· координатные оси можно совмещать, когда нет или мало осей симметрии, с нормалями к плоскостям симметрии;

· координатные оси при отсутствии элементов симметрии или их недостаточном количестве, а это характерно для триклинной и моноклинной сингонии, можно совмещать с осями наиболее развитых зон или, что то же самое, параллельно ребрам кристаллов.