2015-05-12
1420
Цифровой логический уровень находится в самом низу иерархии компьютера. Его еще называют аппаратным обеспечением компьютера. Базовые элементы, из которых конструируются компьютеры, просты. Цифровые схемы могут создаваться из небольшого числа простых элементов путем сочетания этих элементов в различных комбинациях. Цифровой схемой называется схема, в которой есть только два логических значения – 0 и 1. Обычно сигнал от 0 до 1 В представляет одно значение, допустим 0, а сигнал от 2 до 5 В – другое значение, например, 1. Простейшие функции от этих двузначных сигналов вычисляют логические элементы - основа аппаратного обеспечения, на которой строятся все цифровые компьютеры [1]. Логические элементы, в свою очередь, построены на основе транзисторов. В зависимости от выбранной производственной технологии: биполярной или МОП (металл-оксид-полупроводник) – элемент, выполняющий одну и ту же логическую функцию, может выглядеть по-разному.
Среди биполярных технологий отметим ТТЛ (транзисторно-транзисторную логику) и ЭСЛ (эмиттерно-связанную логику). Современные процессоры и память, которые являются наиболее сложными цифровыми схемами, чаще всего производят с использованием технологии комплиментарных МОП (КМОП), которая работает при напряжении 3,3 В, занимает гораздо меньше места по сравнению с биполярной технологией и потребляет меньшее количество энергии.
|
|
|
На схемах логические элементы отображают в виде прямоугольников с выводами слева и справа. С левой стороны прямоугольников рисуют входы логического элемента, а с правой стороны – выходы. Внутри прямоугольника вносят условное обозначение логической функции, выполняемой данным элементом. Небольшие окружности в основании выводов обозначают инвертирование сигнала.
На рис.3.1а приведены основные виды логических элементов, которые нам понадобятся при выполнении лабораторной работы.
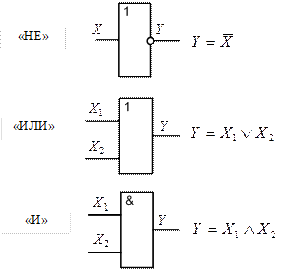
Рис.3.1а. Схематическое обозначение основных видов логических элементов.
Кроме аналитического задания логических функций, то есть с помощью формул, существует еще табличный способ. При табличном способе строится так называемая таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие им значения логической функции.
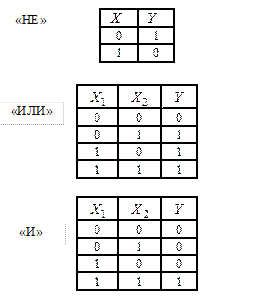
Рис.3.1б. Табличный способ задания основных логических элементов.
Более сложные логические функции формируются путем сочетания различных логических элементов с помощью особой алгебры – алгебры логики, в которой все переменные и функции могут принимать только одно из двух возможных значений: 0 и 1. Поэтому логическая функция от n переменных имеет только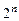 
возможных комбинаций значений переменных. Такую функцию можно полностью описать в таблице с 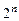строками. В каждой строке будет даваться значение функции для разных комбинаций значений переменных. Такая таблица называется таблицей истинности.
|
|
|
В качестве примера рассмотрим таблицу истинности для функции "большинства трех переменных". Значение функции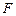 
принимает значение 1 в том случае, когда в комбинации из трех переменных 
, 
, 
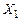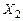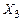единиц больше, чем нулей.
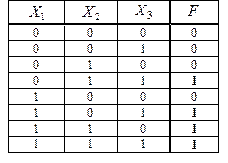
Рис.3.2. Таблица истинности функции "большинства трех переменных"
Для упрощения записи выражений будем использовать знак «·» вместо знака «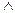
», и «+» вместо знака «
».
Существует четыре комбинации переменных, для которых функция принимает значение 1: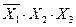 
(4-ая строка в таблице истинности), 
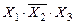(6-ая строка), 
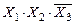(7-ая строка) и 
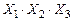(8-ая строка). Черта ставится над переменными, значения которых в данной комбинации равны нулю. Функция 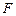принимает значение 1, если одна из этих комбинаций истинна. Следовательно, можем записать выражение для функции:
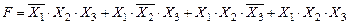(Ф.3.1)
Для программирования логических функций на языке Си необходимо использовать битовые операторы, которые соответствуют логическим операторам дискретной математики (ДМ):
Таблица 3.1. Битовые операторы.
| Оператор языка Си | Оператор ДМ | Значение | Тип | Описание |
| & |
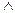| and | бинарный | и |
| | |
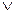| or | бинарный | или |
| ~ | 
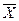| not | унарный | не (отрицание) |
Согласно таблице 3.1 формулу Ф.3.1 можно представить в виде оператора присваивания f=~x1&x2&x3|x1&~x2&x3|x1&x2&~x3|x1&x2&x3. Полностью программа, реализующая функцию большинства трех переменных, приведена в примере 3.1.
Пример 3.1. Функция большинства трех переменных.
#include <conio.h>
#include <stdio.h>
void main()
{
clrscr();
char x1,x2,x3,f;
printf("\n X1 X2 X3 F");
for (x1=0;x1<=1;x1++)
for (x2=0;x2<=1;x2++)
for (x3=0;x3<=1;x3++)
{
f=(~x1&x2&x3|x1&~x2&x3|x1&x2&~x3|x1&x2&x3) & 1;
printf("\n %d %d %d = %d",x1,x2,x3,f);
}
getch();
}
Из-за того, что в языках высокого уровня не существует тип переменных длиной в 1 бит, поэтому используется обрезка переменной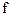 
до нулевого бита (крайнего справа) с помощью действия & 1.
По формуле функции создаем ее схему на логических элементах. Для упрощения создаваемой схемы вместо элементарных двухвходовых элементов по мере надобности будем использовать трех- и четырехвходовые.
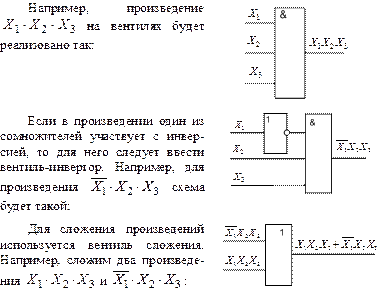
По формуле Ф.3.1. видно, что в нашей схеме есть три инвертора для реализации элементов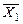 
, 
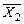и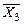 
, четыре трехвходовых логических элементов "И" и один четырехвходовый сумматор для получения результирующей функции .
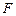На рисунке 3.3 показана полученная схема.
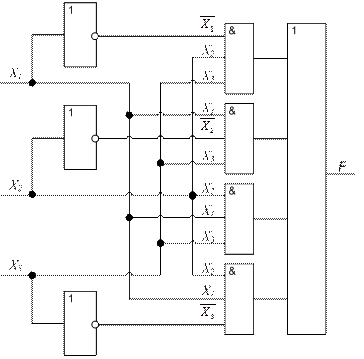
Рис.3.3. Схема функции большинства трех переменных
на элементах И-ИЛИ-НЕ.
Часто реализация функции, записанной напрямую по таблице истинности, не дает оптимальный вариант решения. Для упрощения функций можно использовать карту Вейча [4]. Карта Вейча определяет значения функции на всех возможных наборах значений аргументов, но отличается от таблицы истинности более компактной формой записи.
Для нашего случая размер карты Вейча –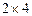 
(рис. 3.4), т.к. таблица истинности имеет всего 
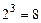значений.
Рис.3.4. Пустая карта Вейча для функции трех переменных.
Заполним карту Вейча по следующему правилу обхода: последовательно сначала до конца из таблицы истинности (рис. 3.2) значения функции заносятся в карту по стрелкам обхода карты (рис. 3.5.).
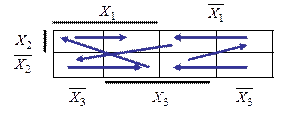
Рис.3.5. Порядок обхода карты Вейча .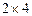
В заполненной карте Вейча выделяем рядом стоящие единицы в группы по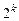 
клеток (рис. 3.6). Выделение следует проводить либо по горизонтали, либо по вертикали. Диагональ группу не образует.
Рис.3.6. Заполненная карта Вейча для функции
"большинства трех переменных" с выделенными группами.
Для полученных групп по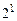 
клеток определяем набор аргументов:
· для группы 1 соответствует произведение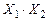 
; аргумент 
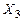здесь не присутствует, т.к. он присутствует для одной клетки с инверсией, а для другой – без инверсии.
|
|
|
· для группы 2: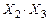 
;
· для группы 3: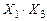 
.
Таким образом, можно записать минимизированную функцию:
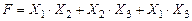
Доказано, что минимизация, проведенная с помощью карты Вейча, дает в результате минимально дизъюнктивную нормальную форму (МДНФ).
Схема функции на логических элементах минимизированной функции будет такой:
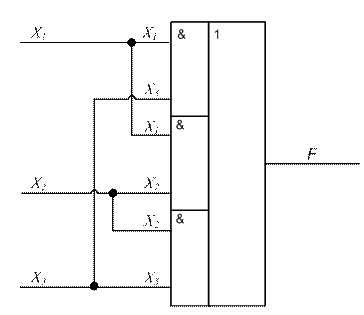
Рис.3.7. Схема минимизированной функции
большинства трех переменных на элементах И-ИЛИ.
Пример 3.2. Минимизированная функция большинства трех переменных.
#include <conio.h>
#include <stdio.h>
void main()
{ clrscr();
char x1,x2,x3,f;
printf("\n X1 X2 X3 F");
for (x1=0;x1<=1;x1++)
for (x2=0;x2<=1;x2++)
for (x3=0;x3<=1;x3++)
{ f=(x1&x2|x2&x3|x1&x3) & 1;
printf("\n %d %d %d = %d",x1,x2,x3,f);}
getch();}
