2015-05-12
287
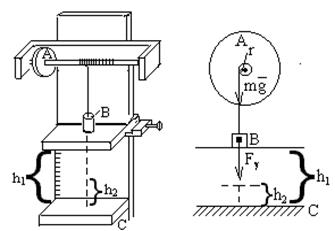
Сущность метода заключается в нахождении момента инерции твердого тела, используя законы динамики. Пусть тело A, момент инерции которого мы должны определить, закреплено на оси радиусом r.
К данной оси на нити подвешен груз B массой m. Если в начальный момент времени груз m покоится относительно нижней площадки C на высоте h1 (рис.3) и тело А тоже
Рис.3 покоится, то энергетическое состояние системы AB относительно площадки C будет определяться уравнением:
.
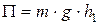Если из-под тела B убрать опору, то оно, падая под действием силы тяжести Fg = mg, приведет тело A во вращение и в момент удара тела B о площадку C с учетом сил трения энергетическое состояние системы AB будет определяться уравнением:
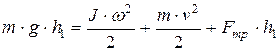, (12)
где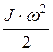 
- кинетическая энергия тела А; 
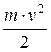- кинетическая энергия тела В; 
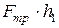- работа сил трения на пути h1.
В результате неупругого удара о площадку С за счет энергии тела А груз В с учетом сил трения поднимется на высоту h2. В этом случае энергетическое состояние системы АВ определится уравнением:
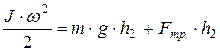(13)
Необходимо учесть связь линейных и угловых кинематических величин при n0 = 0 на высоте h1,
|
|
|
, 
, 
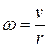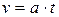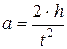, т.е. 
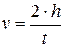, а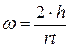 
Тогда решая систему из уравнений (12) и(13) относительно силы трения, найдем:
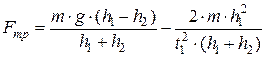(14)
и, подставляя ее значение в уравнение ( 13 ), решая его относительно момента инерции, получим:
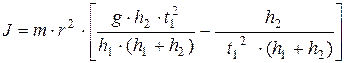(15)
Нетрудно заметить, что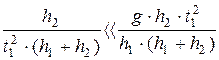 
то уравнение (15)можно записать: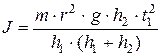 
(16)
Это уравнение и является рабочей формулой данной лабораторной работы.
