Метод проецирования тренда

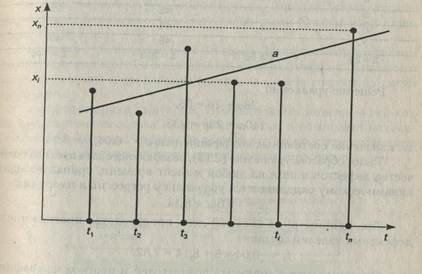
Основной идеей этого метода является построение прямой, кото­рая «в среднем» наименее уклоняется от массива точек (t,x)заданно­го временного ряда (рис. 2.10), описываемого уравнением

х = аt +b, _(2.13)

где а,b — постоянные коэффициенты.

Коэффициент β обычно выбирают методом проб и ошибок с учетом практической деятельности.

Допустим, что на первый день работы в цехе прогноз дефектов был равен 8. Тогда прогноз по каждому следующему дню от предшествующего можно сосчитать по формуле (2.12). Результаты расчета сводим в табл. 2.9.

Отразим полученные результаты и на графике (рис. 2.9). Как видно из графика, прогнозируемый тренд более сглажен, чем на рис. 2.8

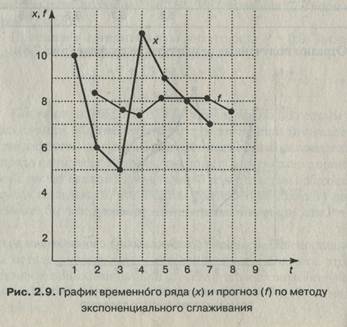
Рис. 2.10. Регрессионная тенденция тренда (а)

Расчет коэффициентов а и b ведется по методу наименьших квад­ратов, т.е. решается система уравнений

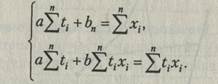(2.14)

Эта система имеет единственное решение. Допустим, что массив данных (t,x), принятый ранее (см. анализ временных рядов), сохраняется. Для расчета коэффициентов заполним таблицу (табл. 2.10).

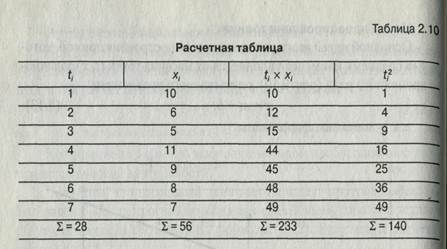
Решение уравнений

28а + 7b = 56,

140а + 28b= 233

даст значение постоянных коэффициентов а = -0,04, b= 8,14.

Таким образом, уравнение (2.13), позволяющее дать прогноз количества дефектов в цехе на любой момент времени, принадлежащий динамическому ряду, является уравнением регрессии и имеет вид

х = -0,04t + 8,14.

Так, например, на восьмой день производства прогноз числа дефектных изделий составит

f₈ = -0,04x8 + 8,14 = 7,82.

Отразим массив реальных показателей и прогноз на графике (рис. 2.11).

Следует отметить, что приведенные методы не исчерпывают все­го многообразия методов анализа временных рядов.