Если в среде распространяется несколько волн, то результирующее колебание каждой частицы среды представляет собой сумму колебаний, которые совершала бы частица от каждой волны в отдельности. Это утверждение называется принципом суперпозиции (наложения) волн.
Интерференцией называется явление наложения когерентных волн, при котором происходит перераспределение энергии колебаний в пространстве, в результате чего в одних его точках наблюдается ослабление, а в других – усиление колебаний.
Когерентными называются колебания (волны, источники), у которых:
1) частоты одинаковые: w 1 = w 2 = w 0;
2) колебания происходят вдоль одного направления (сонаправлены);
3) разность фаз колебаний не изменяется во времени:
d = a2 – a1= сonst
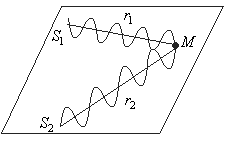
Рис. 1.80
Рассмотрим (рис. 1.80) два когерентных источника S 1 и S 2, от которых распространяются волны так, что в точке наблюдения (точка М) колебания описываются выражениями
S 1(t) = A1 cos (w t – k r 1) = A1 cos (w t – a1)
S 2(t) = A2 cos (w t – k r 2) = A2 cos (w t – a2)
где r 1 и r 2 – расстояния от источников до точки наблюдения a1 и a2 – начальные фазы колебаний в точке наблюдения.
В соответствии с теоремой косинусов амплитуда результирующего колебания в точке М имеет вид:
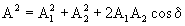
где d = a2 – a1 – разность фаз колебаний в этой точке.
Из этой формулы следует, что:
1) если d = + 2pn, (cos d = 1), то амплитуда колебаний становится максимальной (A = Amax), т. е. в точке пространства, для которой выполняется указанное условие для d происходит усиление колебаний;
2) если d = + (2n+1)p, (cos d = –1), то амплитуда колебаний становится минимальной (A = Amin), т. е. в точке пространства, для которой выполняется указанное условие для d происходит ослабление колебаний. В частности, если А1 = А2, то колебаний не происходит вообще – данная частица среды покоится.
Рассмотрим наиболее простой и важный случай интерференции: сложение двух плоских волн, имеющих одинаковую амплитуду и распространяющихся навстречу друг другу. Возникающий при этом колебательный процесс называется стоячей волной.
Волна, распространяющаяся в положительном направлении оси х:
S 1 = A cos (w t – kх)
Волна, распространяющаяся в отрицательном направлении оси х:
S 2 = A cos (w t + kх)
Результирующая волна получается при сложении
S = S 1 + S 2
Из тригонометрии известно:
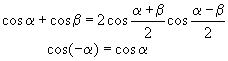
Поэтому
S = S 1 + S 2 = 2A cos kx cosw t,
т. е. амплитуда результирующих колебаний является функцией координаты точки пространства, в которой рассматривается колебание
Aрез = А (х) = 2 A cos kx
Анализ выражения Aрез = 2A cos kx
1) если cos kx = 0, то A рез = 0, т.е. точки среды не колеблются (рис. 1.81). Координаты x = x узл точек среды, в которых колебания отсутствуют, называются узлами:
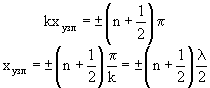
(n = 0, 1, 2,...)
2) если cos kx = + 1, то A рез = Аmax, т. е. амплитуда колебаний соответствующих точек среды максимальна (рис. 1.81). Координаты x = х пучн точек среды, в которых колебания имеют максимальную амплитуду, называются пучностями:
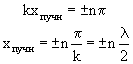
(n = 0, 1, 2,...)
Из этих формул видно, что расстояние между соседними пучностями и соседними узлами одинаковое и равно l/2. Все точки, лежащие по разные стороны узлов колеблются в противофазе, а все точки, находящиеся между узлами, колеблются в одинаковой фазе.
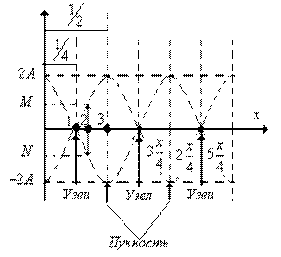
Рис. 1.81
 2015-05-12
2015-05-12 944
944








