Определение. Событие 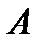 называется зависимым от события
называется зависимым от события 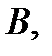 если вероятность события
если вероятность события 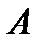 зависит от того, произошло событие
зависит от того, произошло событие 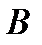 или нет.
или нет.
Определение. Вероятность события 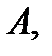 вычисленная при условии, что событие
вычисленная при условии, что событие 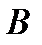 произошло, называется условной вероятностью события
произошло, называется условной вероятностью события 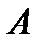 и обозначается
и обозначается 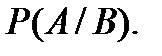
Теорема. Вероятность произведения событий 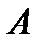 и
и 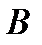 равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
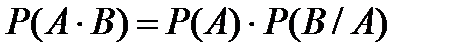 или
или 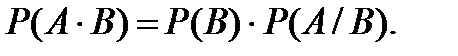 (3.14)
(3.14)
Условие независимости события 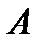 от события
от события 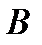 можно записать в виде
можно записать в виде 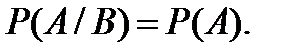 Из этого утверждения следует, что для независимых событий выполняется соотношение:
Из этого утверждения следует, что для независимых событий выполняется соотношение:
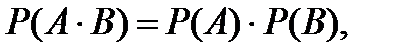 (3.15)
(3.15)
т. е. вероятность произведения независимых событий 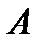 и
и 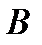 , равна произведению их вероятностей.
, равна произведению их вероятностей.
Замечание. Вероятность произведения нескольких событий 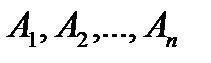 равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:
равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:
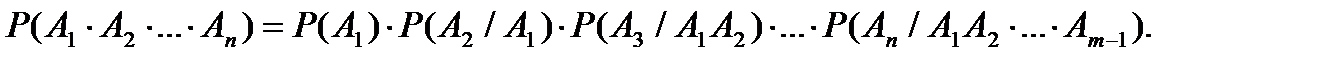
Если события независимые, то имеем:
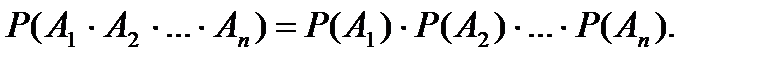
Пример 3.31. В ящике 5 белых и 3 черных шара. Из него наугад последовательно без возвращения вытаскивают два шара. Найти вероятность того, что оба шара белые.
Пусть событие 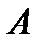 − появление белого шара при первом вынимании,
− появление белого шара при первом вынимании, 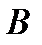 − появление белого шара при втором вынимании. Учитывая, что
− появление белого шара при втором вынимании. Учитывая, что 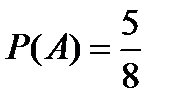 ,
, 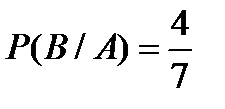 (вероятность появления второго белого шара при условии, что первый вынутый шар был белым и его не возвратили в ящик). Так как события
(вероятность появления второго белого шара при условии, что первый вынутый шар был белым и его не возвратили в ящик). Так как события  и
и  зависимые, то вероятность их произведения найдем по формуле (3.15):
зависимые, то вероятность их произведения найдем по формуле (3.15):
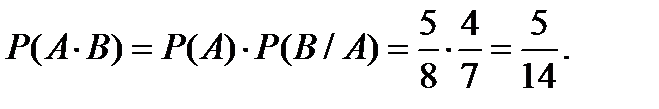
Пример 3.32. Вероятность попадания в цель первым стрелком 0,8; вторым – 0,7. Каждый стрелок выстрелил по мишени. Какова вероятность того, что хотя бы один стрелок попадет в цель? Какова вероятность того, что один стрелок попадет в цель?
Пусть событие 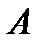 – попадание в цель первым стрелком,
– попадание в цель первым стрелком, 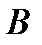 – вторым. Все возможные варианты можно представить в виде таблицы 3.5, где «+» обозначает, что событие произошло, а «−» − не произошло.
– вторым. Все возможные варианты можно представить в виде таблицы 3.5, где «+» обозначает, что событие произошло, а «−» − не произошло.
Таблица 3.5
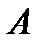 | 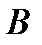 |
| + | + |
| + | − |
| − | + |
| − | − |
Пусть событие 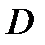 – попадание хотя бы одним стрелком в цель, Тогда событие
– попадание хотя бы одним стрелком в цель, Тогда событие 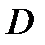 является суммой независимых событий
является суммой независимых событий 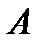 и
и 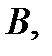 следовательно, применить теорему о вероятности суммы несовместных событий в данной ситуации нельзя.
следовательно, применить теорему о вероятности суммы несовместных событий в данной ситуации нельзя.
Рассмотрим событие 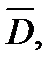 противоположное событию
противоположное событию 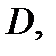 которое произойдет тогда, когда ни один стрелок не попадет в цель, т. е. является произведением независимых событий
которое произойдет тогда, когда ни один стрелок не попадет в цель, т. е. является произведением независимых событий 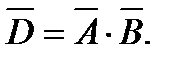 Используя формулы (3.13) и (3.15), получим:
Используя формулы (3.13) и (3.15), получим:
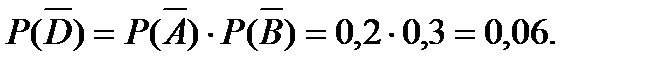
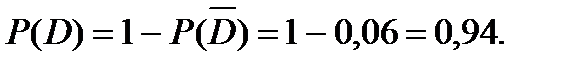
Пусть событие 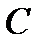 – попадание одним стрелком в цель. Это событие можно представить следующим образом:
– попадание одним стрелком в цель. Это событие можно представить следующим образом:
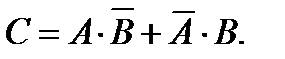
События 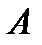 и
и 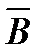 – независимые, события
– независимые, события 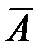 и
и 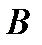 также являются независимыми. События, являющиеся произведениями событий
также являются независимыми. События, являющиеся произведениями событий 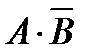 и
и 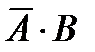 – несовместными. Используя формулы (3.10) и (3.15) получим:
– несовместными. Используя формулы (3.10) и (3.15) получим:
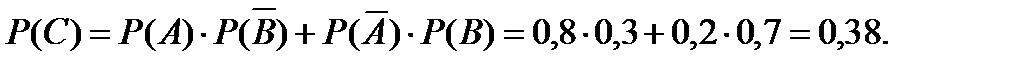
Свойства операций сложения и умножения событий:
1. 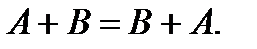
2. 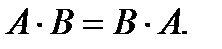
3. 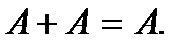
4. 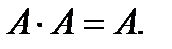
5. 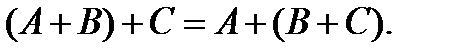
6. 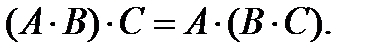
7. 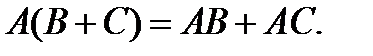
 2015-05-12
2015-05-12 869
869








