Задача. Построение линии пересечения двух плоскостей (поверхностей первого порядка) общего положения Г (АВС) и 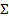 (DEF). Возьмем, например, горизонтальную плоскость уровня и составим алгоритм в символической записи для определения точки M. 1) (DEF). Возьмем, например, горизонтальную плоскость уровня и составим алгоритм в символической записи для определения точки M. 1) 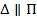 1 1 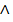 Г (АВС) Г (АВС) 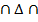 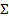 (DEF) 2) Г (АВС) (DEF) 2) Г (АВС) 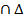 = (A - 1) = (A - 1) 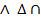 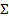 (DEF) = (2 - 3); 3) (A - 1) (DEF) = (2 - 3); 3) (A - 1) 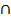 (2 - 3) = M. (2 - 3) = M. | 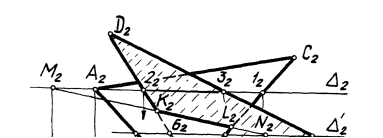 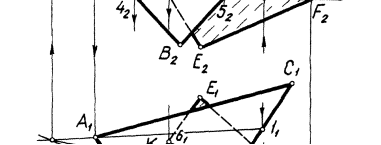 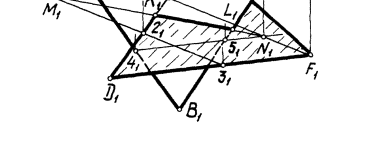 | ||
| 37) Построить точку К пересечения прямой DE c плоскостью α(АВС). | 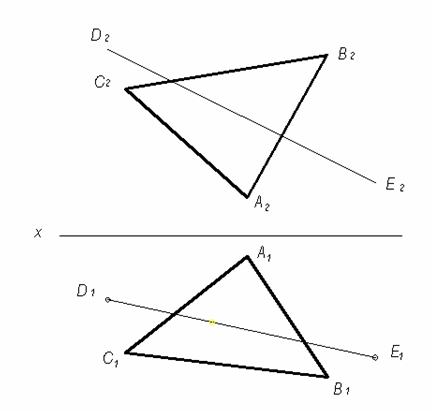 | ||
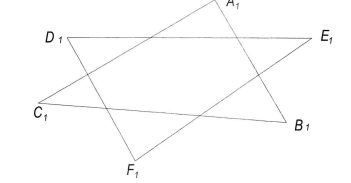
| 38) Построить линию пересечения МN плоскостей α(АВС) и β(DEF) | 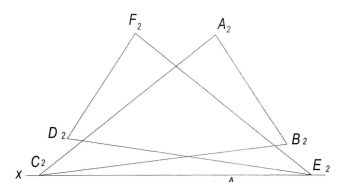 | ||
 | |||
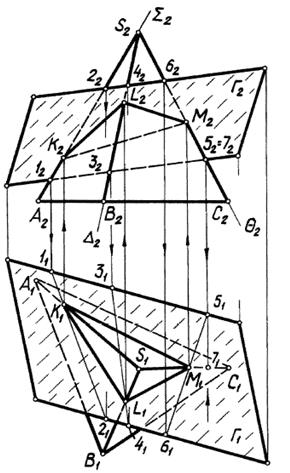 |
Задача. Построение линии пересечения многогранника с плоскостью.
Линия пересечения многогранника с плоскостью является плоской ломаной линией, вершины которой — точки пересечения ребер, а стороны — линии пересечения граней многогранника с плоскостью.
Построение вершин К, L и М ломаной выполнено по алгоритму первой позиционной задачи. Например, алгоритм для определения точки К= Г 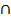 (SA) имеет вид:
(SA) имеет вид:
1) (SA) 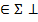 П2;
П2;
2) Г 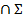 = (1 - 2);
= (1 - 2);
3) (1-2) 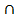 (SA) =K.
(SA) =K.
| 39) Построить точки пересечения прямой общего положения с поверхностью пирамиды. |  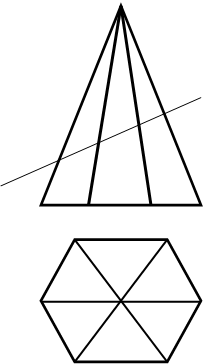  |
Точки L и М определены аналогично. Полученные проекции вершин соединены прямыми с учетом их видимости относительно П1 и П2.
| 40) Построить точки пересечения прямой АВ с поверхностью призмы. | 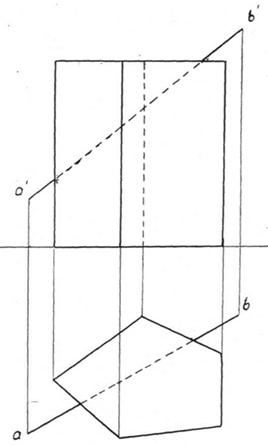 |
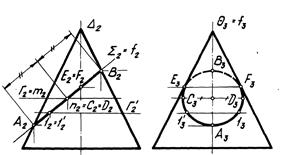
Задача. Построение линии пересечения кривой поверхности с плоскостью.
 | |
 |
Линия l пересечения кривой поверхности Ф с плоскостью 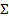 представляет собой плоскую кривую.
представляет собой плоскую кривую.
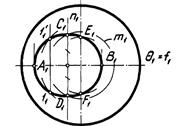
На рисунке показано построение линии пересечения поверхности Ф конуса вращения фронтально проецирующей плоскостью 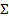 , пересекающей все образующие конуса. Линией пересечения в данном случае является эллипс, для построения проекций которого найдены все опорные точки и ряд промежуточных.
, пересекающей все образующие конуса. Линией пересечения в данном случае является эллипс, для построения проекций которого найдены все опорные точки и ряд промежуточных.
Проведена вспомогательная плоскость 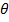 1 = f1. Отмечены фронтальные проекции А2 и В2 искомых точек А и В в пересечении очерка фронтальной проекции конуса (проекции главного меридиана) и фронтальной проекции f2 =
1 = f1. Отмечены фронтальные проекции А2 и В2 искомых точек А и В в пересечении очерка фронтальной проекции конуса (проекции главного меридиана) и фронтальной проекции f2 = 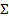 2 фронтали f. Затем, по линиям связи найдены горизонтальные А1, В1 и профильные А3, В3 проекции точек А и В из условия принадлежности их плоскости
2 фронтали f. Затем, по линиям связи найдены горизонтальные А1, В1 и профильные А3, В3 проекции точек А и В из условия принадлежности их плоскости 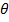 .
.
Точки Е и F (очерковые относительно П3) определены по аналогичному алгоритму. Они являются точками смены видимости проекции эллипса на П3.
Вспомогательная плоскость является общей плоскостью симметрии для конуса Ф и плоскости 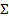 . Поэтому найденные очерковые точки А и В являются одновременно и экстремальными — высшей и низшей относительно П1, наиболее и наименее удаленными относительно П3. Они ограничивают большую ось [АВ]
. Поэтому найденные очерковые точки А и В являются одновременно и экстремальными — высшей и низшей относительно П1, наиболее и наименее удаленными относительно П3. Они ограничивают большую ось [АВ]
эллипса, которая проецируется на П2 в отрезок [A2B2] 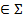 2.
2.
Точки C и D (наиболее и наименее удаленные относительно П2) ограничивают малую ось [CD] эллипса, которая является отрезком фронтально проецирующей прямой n. На П2 она проецируется в точку n2, делящую отрезок [А2В2] пополам. Для по-
строения точек С и D в качестве вспомогательной выбрана горизонтальная плоскость уровня Г 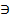 n, пересекающая конус Ф по окружности m, а плоскость
n, пересекающая конус Ф по окружности m, а плоскость 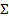 — по прямой n.
— по прямой n.
Алгоритм в символической записи имеет вид:
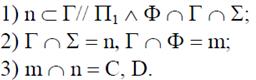
| 41) Построить проекции сечения пирамиды проецирующей плоскостью α | 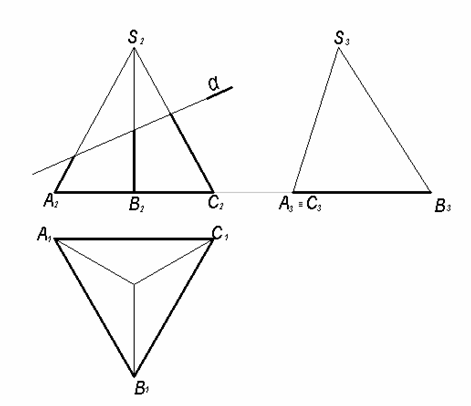 |
| 42) Построить точки пересечения плоскости с поверхностью конуса. | 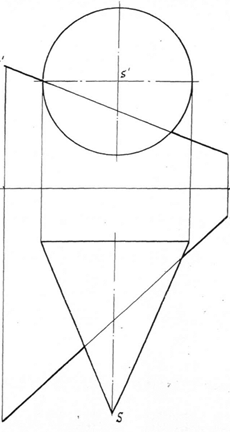 |
| 43) Построить проекции линии пересечения двух многогранников | 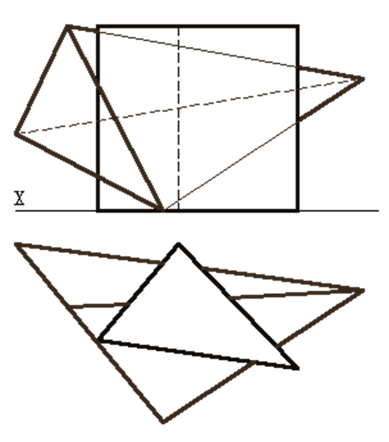 |
44) Построить линию пересечения сферы с фронтально проецирующей плоскостью. 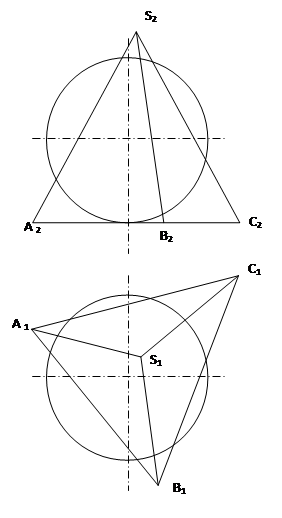 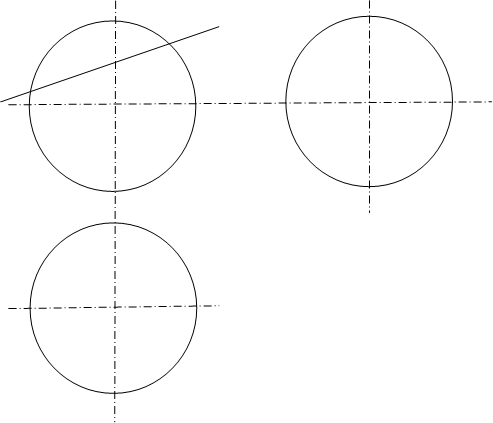
|
 2015-05-12
2015-05-12 1172
1172
