1. 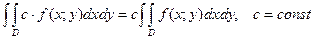
2. 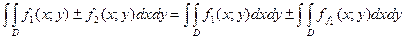
3. Если область  разбить линией на две области
разбить линией на две области  и
и 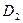 , то
, то

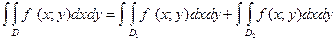
4.Если в области 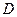 имеет место неравенство
имеет место неравенство 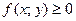 , то и
, то и 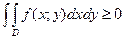 . Если в области
. Если в области 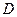 функции
функции 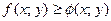 то и
то и 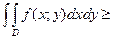
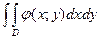 .
.
5. Если подынтегральная функция 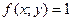 , то двойной интеграл численно равен площади области интегрирования:
, то двойной интеграл численно равен площади области интегрирования:
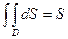 .
.
6. Если функция 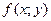 непрерывна в замкнутой области
непрерывна в замкнутой области 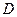 , площадь которой S, то
, площадь которой S, то

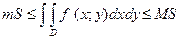 , где
, где 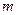 и
и 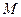 - соответственно наименьшее и наибольшее значение подынтегральной функции в области
- соответственно наименьшее и наибольшее значение подынтегральной функции в области 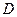 .
.
7. Если функция 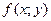 непрерывна в замкнутой области
непрерывна в замкнутой области 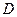 , площадь которой S, то в этой области существует такая точка
, площадь которой S, то в этой области существует такая точка 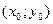 , что
, что
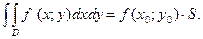
Величину 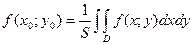 называютсредним значением функции
называютсредним значением функции 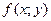 в области
в области 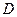 .
.
8. Координаты центра тяжести однородной пластинки можно вычислить по формулам
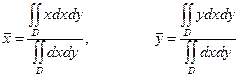 ,
,
Пример 4. Найти координаты центра тяжести фигуры, ограниченной линиями 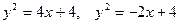 .
.
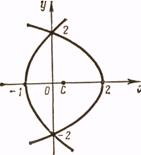
Рис.1
Решение. Так как фигура симметрична относительно оси  , то
, то 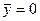 . Остается найти
. Остается найти 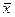 . Найдем площадь фигуры:
. Найдем площадь фигуры:
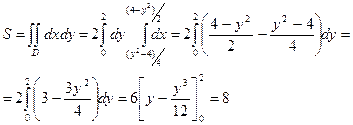
Тогда 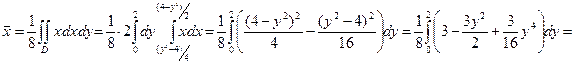
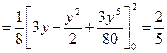 .
.
Пример 5. Изменить порядок интегрирования в двойном интеграле
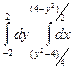 .
.
Решение. Область интегрирования представляет собой фигуру, изображенную на рис. 1. Для изменения порядка интегрирования разобьем область на две части: 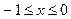 и
и 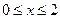 . Тогда исходный интеграл разбивается на сумму двух интегралов:
. Тогда исходный интеграл разбивается на сумму двух интегралов:
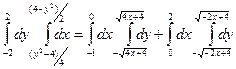
 2015-05-12
2015-05-12 694
694








