2015-05-12
640
Пусть в замкнутой области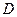 
плоскости 
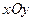задана непрерывная функция 
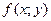.Разобьём область 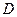на n «элементарных областей»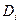 
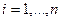, площади которых обозначим через 
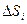, а диаметры (наибольшее расстояние между точками области) через 
.
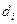В каждой области 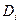выберем произвольную точку 
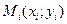, умножим значение 
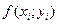функции в этой точки на 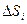и составим сумму всех таких произведений:
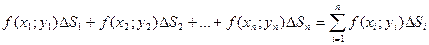
Эта сумма называется функции 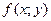в области .
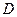Если существует предел интегральной суммы, не зависящий от способа разбиения области 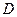на части и выбора точек в них, то он называется двойным интегралом от функции 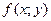по области 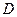и обозначается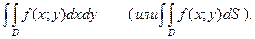 
Таким образом,двойной интеграл определяется равенством
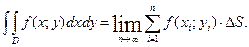
В этом случае функция 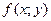называетсяинтегрируемой в области 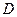; 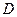- область интегрирования; 
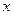и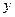 
- переменные интегрирования; 
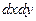или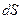 
- элемент площади.
