Цель работы. 1. Написать исходный код своей первой программы для VC++ ver.6.0

1. Написать исходный код своей первой программы для VC++ ver.6.0.

2. Найти и проанализировать лексемы, используемые в исходном коде.

3. Изучить формат функций вывода.

Отчет по лабораторной работе должен содержать:

1. Постановку задачи (цель работы, задание).

2. Алгоритм решения задачи (словесный или в виде блок-схемы, обозначения переменных, используемых при решении задач).

3. Исходный код программы с необходимыми комментариями (исходный код должен использовать стиль программирования).

4. Результаты работы программы (скопированные с экрана дисплея).

5. Анализ полученных результатов, выводы.

6. Описание типов лексем, используемых в исходном коде.

7. Описание формата функции printf().

Задание

Вычислить значение функции y = f(x), предварительно выполнив действия над целыми переменными. Разработать исходный код на языке С, используя главную функцию main() и библиотечную функцию printf() (для вывода всех входных и выходных данных), а также необходимые директивы препроцессора, откомпилировать исходный код, выполнить его компоновку и запустить на выполнение exe-файл.

Выписать размер исходного кода (*.cpp), объектного кода (*.obj) и исполняемого файла (*.exe). Подробно изучить и описать формат функции printf(). Действия над переменными выполнить вручную с использованием двоичной системы координат, результаты сравнить с полученными на ЭВМ.

Дать краткий анализ директив процессора, используемых в исходном коде.

Замечания

1. Если при вычислении квадратного корня подкоренное выражение отрицательно, взять его модуль.

2. Если при вычислении арксинуса (арккосинуса) аргумент х больше единицы, взять в качестве аргумента его обратную величину, т.е. 1/х.

3. При создании простого консольного приложения с помощью мастера проектов Visual C++ Ver 6.0 распечатать файлы проекта.

4. Библиотечные функции см. в приложении 2.

Варианты заданий

Номер вари­анта	Действия над переменными	Функция y = f(x)	Исходные данные
	a=(a--|x<<2)&(a<<2)		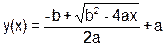a = 5, b = 5, x = 2
	x=(c&x>>1) ^ (x|c>>2)|(x--<<1)		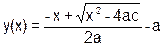a = 3, c = 1, x = 3
	c=(x>>1)|(c<<1) & (--x^c++)		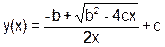b = 3, c = 2, x = 3
	Q=(x&Q-- >>1) | (Q<<1^x<<2)		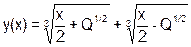Q = 3, x = 3
	q=(++q^x<<1) | (q&x++)		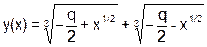x = 2, q = 4
	x=(--x&q<<1) | (x^q++)	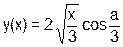, где	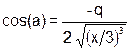x = 4 q = 2
	x=(++x&q) | (x>>1|q--)	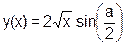, где	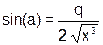x = 3 q = 2
	p=(p|e++>>2) & (++p>>1)		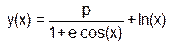p = 3, e = 5, x = p/3
	p=(--p^b--) << (p&b)		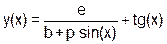p = 3, b = 4, x = p/10
	a=(--a^r++) | (a<<2&r)		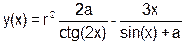r = 2, a = 1, x = p/6
	r=(--r^a) << (r&a++)		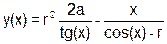r = 1, a = 4, x = p/4
	a=(b|a) ^ (a >>1&b<<1)		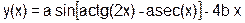a = 4, b = 2, x = p/3
	a=(b|++a) ^ (a<<1&&b--<<1)		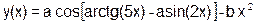a = 3, b = 3, x = p/6
	b=(b|a) << (++b&a++)		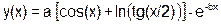a = 1, b = 1, x = p/3
	b=(b|a--) >> (b++&a)		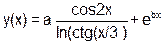a = 3, b = 1, x = p/5
	a=(b&a--) ^ (a<<1|b<<1)		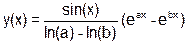a = 3, b = 3, x = p/6
	a=(a^--b) << (a++&b)		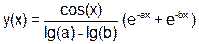a = 1, b = 4, x = p/9
	a=(--a^b++) | (b<<1&a)	y(x) = a×ln(x)×sin(x/2) + b×e2x×cos(x/2)	a = 2, b = 3, x = p/4
	b=(b--&a++)|(b^a)	y(x) = a×lg(x)×cos(x/2) – b×e-x×sin(x/2)	a = 2, b = 4, x = p/9
	a=(a|b++>>1) & (++a>>2)		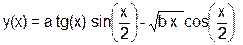a = 5, b = 3, x = p/3
	a=(a++>>1&b) << (a^--b)		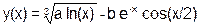a = 3, b = 4, x = p/4
	b=(a>>1&b++) ^ (b>>1|a)		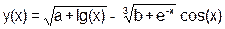a = 4, b = 5, x = p/3
	a=(b&a++) ^ (a|b<<2)		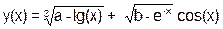a = 2, b = 1, x = p/8
	a=(++b|a>>1) ^ (a&b)		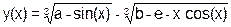a = 3, b = 3, x = p/3
	b=(b&a) | (b++^a>>1)		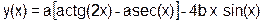a = 4, b = 3, x = p/6

3 Отладка программы с помощью
отладчика Microsoft Visual C++

Программа, свободная от ошибок, есть абстрактное теоретическое понятие. Одно из затруднений, связанных со скрытыми дефектами программ, заключается в том, что вероятность их проявления возрастает со временем и с расширением масштабов использования программы. Мало в какой области деятельности имеется столько возможностей для ошибок, как в программировании. Искусство локализации ошибок, когда факт их существования установлен, носит название отладки.

Одним из критериев профессионального мастерства программистов является способность обнаруживать и исправлять собственные ошибки: начинающие программисты не умеют этого делать, у опытных программистов это не вызывает затруднений.