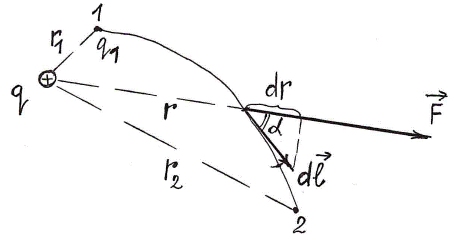
Заряд 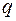 действует на заряд
действует на заряд 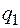 с силой
с силой 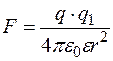 .
.
Переместим 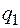 из точки 1 в точку 2. Сила
из точки 1 в точку 2. Сила 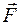 при этом совершает работу:
при этом совершает работу:
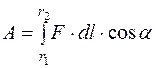 =
= 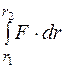 =
= 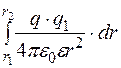
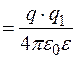
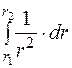 =
=
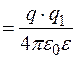
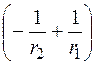 .
. 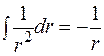
С другой стороны,
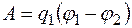 .
.
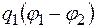
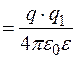
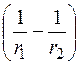 .
. 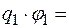
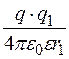 .
.
Опуская индексы:
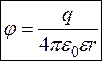 - (11)
- (11)
потенциал поля, созданного точечным зарядом 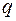 , на расстоянии
, на расстоянии 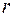 от него.
от него.
Также вне полой заряженной сферы радиусом 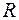 (при
(при 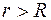 ),
),
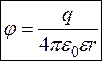 ,
,
Внутри и на поверхности сферы (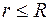 ),
),
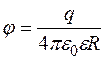 .
.
Принцип суперпозиции полей: напряженность поля, образованного несколькими зарядами, равна сумме напряженностей полей, создаваемых каждым зарядом в отдельности, т.е.
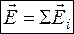 .
.
То же справедливо для потенциала,
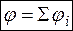 .
.
Теорема Гаусса
1. Поток 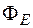 электрического поля через поверхность.
электрического поля через поверхность.
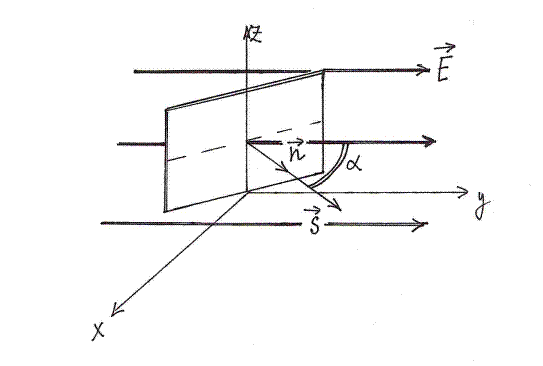
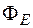
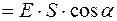 ,
, 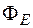
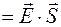 .
.
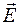 - напряженность электрического поля,
- напряженность электрического поля,
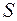 - площадь поверхности,
- площадь поверхности,
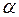 - угол между
- угол между 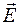 и нормалью
и нормалью 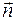 к поверхности,
к поверхности,
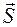 - вектор, численно равный
- вектор, численно равный 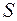 и направленный по нормали к поверхности.
и направленный по нормали к поверхности.
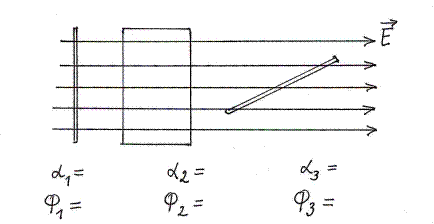
(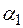 =0,
=0, 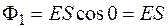 =
= 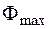 ;
;
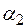 =90°,
=90°, 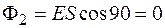 ;
;
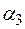 =
= 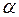 ,
, 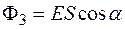 )
)
Величина потока 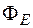 пропорциональна числу силовых линий, пересекающих поверхность.
пропорциональна числу силовых линий, пересекающих поверхность.
Если поверхность имеет сложную форму, то сначала считают поток через элемент поверхности,
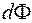
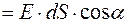 ,
,
а затем через всю поверхность:
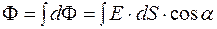 .
.
2. Рассмотрим поток поля точечного заряда через сферическую поверхность радиусом 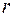 .
.
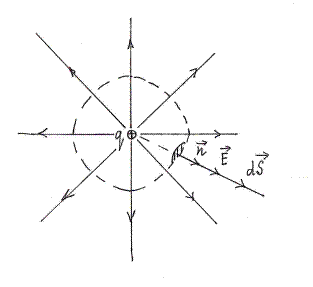
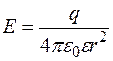 ,
, 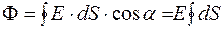
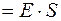 .
.
Для сферы 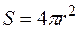 . В итоге,
. В итоге,
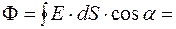
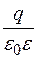 ,
,
Т.е. поток напряженности поля точечного заряда равен заряду внутри нее, деленному на 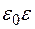 .
.
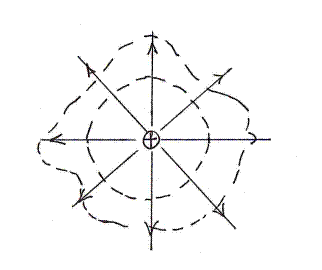
Через произвольную замкнутую поверхность поток останется тем же самым (число силовых линий через обе поверхности одинаково).
Т-ма Гаусса:
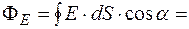
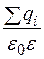 ,
,
Поток напряженности эл поля через произвольную замкнутую поверхность равен сумме зарядов внутри нее, деленной на 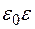 .
.
Т-ма Гаусса применяется для расчета электрических полей.
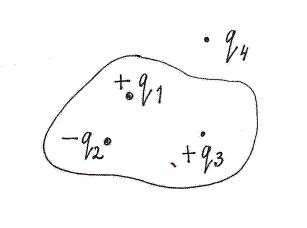
Пример. Поле бесконечной заряженной нити.
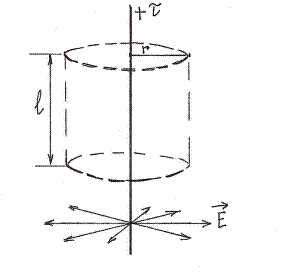
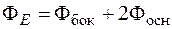 ,
,
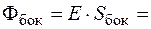
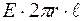 .
.
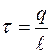 - линейная плотность заряда. [
- линейная плотность заряда. [ 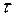 ] =Кл/м.
] =Кл/м.
Заряд внутри цилиндрической поверхности
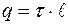 .
.
Т.к. 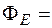
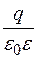 , то
, то 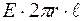
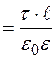 , или,
, или,
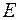
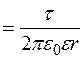 .
.
 2015-05-12
2015-05-12 896
896








