2015-05-13
621
Учитывая, что коэффициент регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, используем коэффициент эластичности (Э) и бета-коэффициент, которые соответственно рассчитываются по формулам:
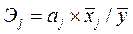
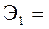9.568´9.294/306.813= 0.2898
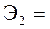15.7529´107.231/306.813= 5.506
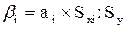
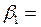9.568´4.913/102.865= 0.457
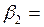15.7529´4.5128/102.865= 0.691
Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на один процент.
Бета-коэффициент с математической точки зрения показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных. Это означает, что при увеличении затрат на рекламу в нашем примере на 4.91 тыс. руб. объем реализации увеличится на 47 тыс. руб. (0.457*102.865).
6. Определить точечные и интервальные прогнозные оценки объема реализации на два квартала вперед (t0,7 = 1,12)
Исходные данные представлены временными рядами, поэтому прогнозные значения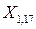 
, 
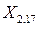и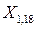 
, 
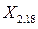можно определить с помощью методов экспертных оценок, с помощью средних абсолютных приростов или вычислить на основе экстраполяционных методов.
Для фактора Х1 Затраты на рекламу выбрана модель
Х1 = 12.83-11.616t +4.319t2 –0.552t3+0.020t4-0.0006t5,
по которой получен прогноз на 2 месяца вперед[1]. График модели временного ряда Затраты на рекламу приведен на Рисунке 4.5.
| Упреждение | Прогноз |
| 5.75 | |
| 4.85 |
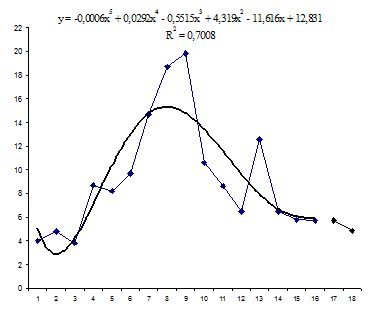
Рисунок 4.5. Прогноз показателя Затраты на рекламу.
Для временного ряда Индекс потребительских расходов в качестве аппроксимирующей функции выбран полином второй степени (парабола), по которой построен прогноз на 2 шага вперед. На рисунке 4.6. приведен результат построения тренда для временного ряда Индекс потребительских расходов.
Х2 = 97.008+1.739t – 0.0488t2.
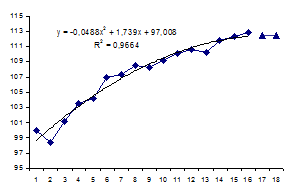
Рисунок 4.6. Прогноз показателя Индекс потребительских расходов.
| Упреждение | Прогноз | |
| 112.468 | ||
| 112.488 |
Для получения прогнозных оценок зависимостей переменной по модели
Y = -1471.438 + 9.568X1 + 15.754X2
подставим в нее найденные прогнозные значения факторов X1 и X2.
Yt=17 = -1471.438 + 9.568*5.75 + 15.754*112.468=355.399
Yt=18 = -1471.438 + 9.568*4.85 + 15.754*112.488=344.179
Доверительный интервал прогноза будет иметь следующие границы:
Верхняя граница прогноза: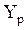 
(n+l)+ U(l),
Нижняя граница прогноза: 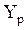(n+ l) - U(l).
u(l) = Se tкр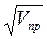 
= Se tкр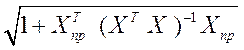 
S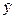 
= 41.473
tкр = 1,77 (Значение tкр получено с помощью функции СТЬЮДРАСПРОБР(0.1;13) для выбранной вероятности 90% с числом степеней свободы равным 13.)
На первый шаг:
l =1
ХпрТ = (1; 5.75; 112.468)
(Xт X)-1 =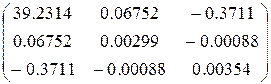 
u(1) = 81,45
На второй шаг:
l=2
ХпрТ = (1; 4.85; 112.488)
u(2) = 82б47
Результаты прогнозных оценок модели регрессии представим в табл. 4.8.
Табл. 4.8.
| Таблица прогнозов (p = 90%) | |||
| Упреждение | Прогноз | Нижняя граница | Верхняя граница |
| 355,399 | 273,94 | 436,85 | |
| 344,179 | 261,71 | 426,65 |
