Статистические данные по всем переменным приведены в таблице 21. В этом примере n = 16, m = 5.
Таблица 21
| Y | Х1 | X2 | X3 | X4 | X5 |
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов |
| 4,8 | 14,8 | 17,3 | 98,4 | ||
| 3,8 | 15,2 | 16,8 | 101,2 | ||
| 8,7 | 15,5 | 16,2 | 103,5 | ||
| 8,2 | 15,5 | 104,1 | |||
| 9,7 | |||||
| 14,7 | 18,1 | 20,2 | 107,4 | ||
| 18,7 | 15,8 | 108,5 | |||
| 19,8 | 15,8 | 18,2 | 108,3 | ||
| 10,6 | 16,9 | 16,8 | 109,2 | ||
| 8,6 | 16,3 | 110,1 | |||
| 6,5 | 16,1 | 18,3 | 110,7 | ||
| 12,6 | 15,4 | 16,4 | 110,3 | ||
| 6,5 | 15,7 | 16,2 | 111,8 | ||
| 5,8 | 17,7 | 112,3 | |||
| 5,7 | 15,1 | 16,2 | 112,9 |
Использование инструмента Корреляция (Анализ данных в EXCEL).
Для проведения корреляционного анализа выполните следующие действия:
1. Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.
2. Выберите команду СервисÞАнализ данных.
3. В диалоговом окне Анализ данных выберите инструмент Корреляция, а затем щелкните на кнопке ОК.
4. В диалоговом окне Корреляця в поле Входной интервалнеобходимо ввести диапазон ячеек, содержащих исходные данные. Если выделены и заголовки столбцов, то установить флажок Метки в первой строке.
5. Выберите параметры вывода. В данном примере Новый рабочий лист.
6. ОК.
Таблица 22
Результат корреляционного анализа.
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов | |
| Столбец 1 | Столбец 2 | Столбец 3 | Столбец 4 | Столбец 5 | Столбец 6 | |
| Объем реализации | ||||||
| Время | 0.678 | |||||
| Реклама | 0.646 | |||||
| Цена | 0.233 | 0.174 | -0.003 | |||
| Цена конкурента | 0.226 | -0.051 | 0.204 | 0.698 | ||
| Индекс потребительских расходов | 0.816 | 0.960 | 0.273 | 0.235 | 0.03 |
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем реализации имеет тесную связь с индексом потребительских расходов (ryx5= 0.816), с расходами на рекламу (ryx2 = 0.646) и со временем (ryx1 = 0.678). Однако факторы Х2 и Х5 тесно связаны между собой (rх 1x5 = 0.96), что свидетельствует о наличии мультиколлинеарности. Из этих двух переменных оставим в модели Х5 - индекс потребительских расходов. В этом примере n = 16, m = 5, после исключения незначимых факторов n = 16, k =2.
2. Выбор вида модели и оценка ее параметров. Оценка параметров регрессии осуществляется по методу наименьших квадратов по формуле 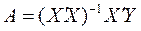 , используя данные, приведенные в таблице 23
, используя данные, приведенные в таблице 23
Таблица 23
| Y | X0 | X1 | X2 |
| Объем реализации | Реклама | Индекс потребительских расходов | |
| 4,8 | 98,4 | ||
| 3,8 | 101,2 | ||
| 8,7 | 103,5 | ||
| 8,2 | 104,1 | ||
| 9,7 | |||
| 14,7 | 107,4 | ||
| 18,7 | 108,5 | ||
| 19,8 | 108,3 | ||
| 10,6 | 109,2 | ||
| 8,6 | 110,1 | ||
| 6,5 | 110,7 | ||
| 12,6 | 110,3 | ||
| 6,5 | 111,8 | ||
| 5,8 | 112,3 | ||
| 5,7 | 112,9 |
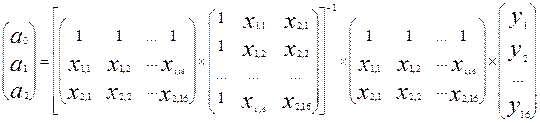

(Xт X) = 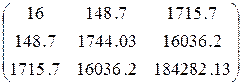
(Xт X)-1 = 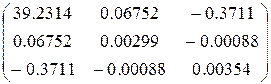
A = (Xт X)-1 X т Y = 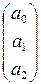 =
= 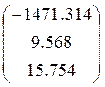
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде:
y = -1471.314 + 9.568х1 + 15.754х2
Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого наблюдения.
Применение инструмента Регрессия (Анализ данных в EXCEL).
Для проведения регрессионного анализа выполните следующие действия:
1. Выберите команду СервисÞАнализ данных.
2. В диалоговом окне Анализ данных выберите инструмент Регрессия, а затем щелкните на кнопке ОК
3. В диалоговом окне Регрессия в поле Входной интервал Y введите адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал Х введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных (Рисунок 4.1.).
4. Если выделены и заголовки столбцов, то установить флажок Метки в первой строке.
5. Выберите параметры вывода. В данном примере Новая рабочая книга
6. В поле Остатки поставьте необходимые флажки.
7. ОК.
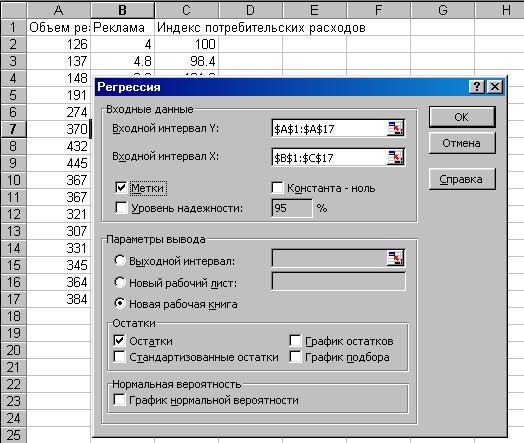
Рис.6. Диалоговое окно Регрессия подготовлено к выполнению анализа данных.
Результат регрессионного анализа содержится в таблицах 24 –27. Рассмотрим содержание этих таблиц.
Таблица 24.
| Регрессионная статистика | |
| Множественный R | 0.927 |
| R-квадрат | 0.859 |
| Нормированный R-квадрат | 0.837 |
| Стандартная ошибка | 41.473 |
| Наблюдения | 16.000 |
Таблица 25
| Дисперсионный анализ | ||||
| df | SS | MS | F | |
| Регрессия | 136358.334 | 68179.167 | 39.639 | |
| Остаток | 22360.104 | 1720.008 | ||
| Итого | 158718.438 |
Таблица 26
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение | -1471.314 | 259.766 | -5.664 |
| Реклама | 9.568 | 2.266 | 4.223 |
| Индекс потребительских расходов | 15.753 | 2.467 | 6.386 |
Таблица 27
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное | Остатки |
| 142,25 | -16,25 | |
| 124,70 | 12,30 | |
| 159,24 | -11,24 | |
| 242,35 | -51,35 | |
| 247,02 | 26,98 | |
| 307,06 | 62,94 | |
| 361,20 | 70,80 | |
| 416,80 | 28,20 | |
| 424,18 | -57,18 | |
| 350,32 | 16,68 | |
| 345,37 | -24,37 | |
| 334,72 | -27,72 | |
| 386,79 | -55,79 | |
| 352,05 | -7,05 | |
| 353,23 | 10,77 | |
| 361,73 | 22,27 |
Пояснения к таблице 24
| Регрессионная статистика | |||
| № | Наименование в отчете EXCEL | Принятые наименования | Формула |
| Множественный R | Коэффициент множественной корреляции, индекс корреляции | 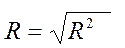
| |
| R-квадрат | Коэффициент детерминации, R2 | 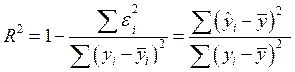
| |
| Нормированный R-квадрат | Скорректированный R2 | 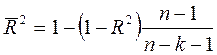
| |
| Стандартная ошибка | Стандартная ошибка оценки | 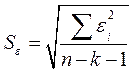
| |
| Наблюдения | Количество наблюдений, n | n |
Пояснения к таблице 25
| Df – число степеней свободы | SS – сумма квадратов | MS | F – критерий Фишера | |
| Регрессия | k =2 | 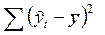
| 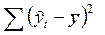 /k /k
| 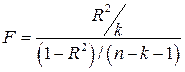
|
| Остаток | n-k-1 = 13 | 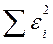
| 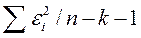
| |
| Итого | n-1 = 15 | 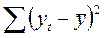
|
Пояснения к таблице 26.
Во втором столбце таблицы 26 содержатся коэффициенты уравнения регрессии a0, a1, a2. В третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, а в четвертом - t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде:
y = -1471.314 + 9.568х1 + 15.754х2
 2015-05-13
2015-05-13 636
636








