Правило знаков для напряжений взаимной

ИНДУКЦИИ

Рассмотрим две катушки взаимной индуктивности, включенные в разные ветви электрической цепи (рис. 5.6). Однополярные зажимы катушек размечены так, что их взаимная индуктивность положительна (для определенности). Направления токов 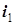и 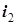были выбраны произвольно, как обычно при составлении уравнений Кирхгофа.

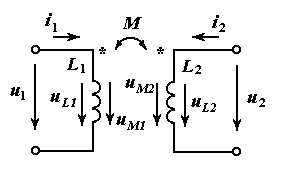
Рис. 5.6. Сравнение направлений напряжений самоиндукции и взаимной индукции в катушках взаимной индуктивности

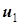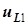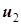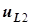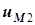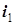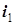Направления напряжений , и , согласованы с направлениями соответствующих токов. Направление напряжения взаимной индукции во второй катушке согласовано с направлением возбуждающего его тока . Ток входит в первую катушку через помеченный зажим, и напряжение 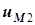направлено на второй катушке от помеченного зажима к непомеченному. Аналогичным образом напряжение взаимной индукции на первой катушке 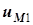согласовано с направлением тока 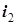. По второму закону Кирхгофа

,

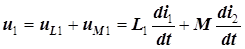(5.7)

.

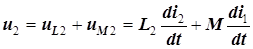На рис. 5.6 токи 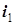и направлены одинаковым образом относительно однополярных зажимов (оба тока входят в катушки через помеченные зажимы). Возможен другой вариант, когда токи и направлены различным образом относительно однополярных зажимов (один ток входит в катушку через помеченный зажим, второй ток выходит из катушки через помеченный зажим) (рис. 5.7).

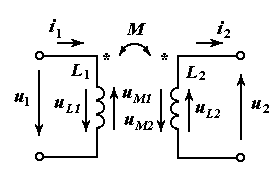
Рис. 5.7. Сравнение направлений напряжений самоиндукции и взаимной индукции в катушках взаимной индуктивности (второй вариант)

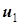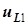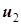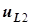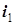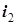Здесь, как всегда, направления напряжений , и , согласованы с направлениями токов и соответственно. По сравнению с рис. 5.6 изменились направления напряжени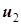й и 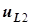вследствие изменения направления тока 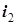. Направление напряжения взаимной индукции во второй катушке 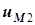согласовано с направлением тока 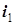. Направление тока 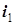осталось таким же, как на рис. 5.6, поэтому сохранилось без изменения направление напряжения 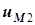. Направление напряжения взаимной индукции в первой катушке 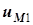согласовано с направлением тока 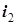(этот ток выходит из помеченного зажима второй катушки и напряжение 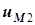направлено от непомеченного к помеченному зажиму первой катушки). По сравнению с рис. 5.6 ток 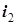изменил направление, и изменилось направление индуцированного им напряжения 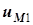. Напряжения на катушках определим по второму закону Кирхгофа:

,

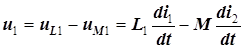(5.8)

.

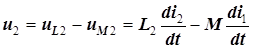На основании уравнений (5.7) и (5.8) можно сформулировать правило знаков для напряжений взаимной индукции.

Первая часть правила соответствует формулам (5.7), а вторая часть – формулам (5.8).

В ходе записи уравнений, составляемых по второму закону Кирхгофа, напряжение, возбуждаемое в каждой катушке переменным магнитным полем, нужно делить на две составляющие: напряжение самоиндукции и напряжение взаимной индукции. Сначала определяется знак перед напряжением самоиндукции (при этом направление напряжения самоиндукции, как обычно, сравнивается с направлением обхода контура, для которого составляется уравнение второго закона Кирхгофа). Затем по правилу И 5.6 определяется знак перед напряжением взаимной индукции.

В системе нескольких катушек взаимной индуктивности напряжение на каждой катушке нужно разделить на несколько составляющих: напряжение самоиндукции и напряжения взаимной индукции по числу катушек, имеющих магнитную связь с рассматриваемой катушкой. Знак перед каждым из напряжений взаимной индукции определяется по правилу И 5.6.

Примечание. В случае, когда взаимная индуктивность является отрицательным числом, правило знаков И 5.6 сохраняется без изменений, потому что не изменяется относительное расположение стрелок, указывающих направления напряжений самоиндукции и взаимной индукции. Поэтому сохраняется вид уравнений (5.7) и (5.8). Разумеется, уравнения с численными значениями параметров в случае положительной и в случае отрицательной взаимной индуктивности будут отличаться друг от друга. Решения уравнений Кирхгофа, одинаковых в общем виде, но различных после подстановки численных значений параметров вследствие различия знаков взаимной индуктивности, будут различными.