Идеальный трансформатор

Идеальный трансформатор обеспечивает передачу электрической энергии из источника в приемник без потерь и без рассеивания в окружающем пространстве. Для этого необходимо выполнение двух условий: 1) в трансформаторе нет потерь электрической энергии, значит, 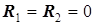; 2) магнитный поток, созданный первичным током, полностью сцеплен со вторичной катушкой (соответственно, магнитный поток, созданный вторичным током полностью сцеплен с первичной катушкой).

Запишем уравнения трансформатора для этого идеального случая:

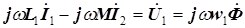, (5.17)

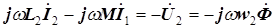. (5.18)

Последние члены в этих соотношениях показывают, что ЭДС, уравновешивающие напряжения 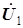и 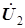, наводятся в первичной и вторичной катушках одним и тем же магнитным потоком 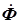; потокосцепления катушек равны

, ,

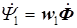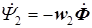где 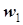и 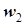- витки первичной и вторичной катушек.

Остается только уточнить знаки. Обратимся к рис. 5.16, где изображены две катушки, помещенные на магнитный сердечник. Однополярные зажимы размечены так, что взаимная индуктивность катушек положительна. Направления токов и напряжений выбраны так же, как на схеме трансформатора (рис. 5.12). С каждой катушкой связана правовинтовая система координат, т.е. ток и магнитный поток в каждой катушке связаны правилом правого винта; в этих системах координат определены направления, во - первых, магнитных потоков 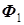и 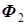и, во - вторых, напряжений на первой катушке 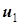и на второй катушке 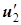, последнее отличается от ранее выбранного напряжения 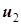знаком. 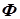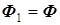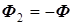Пусть направление магнитного потока в сердечнике совпадает с направлением магнитного потока , при этом и , соответственно 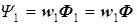и .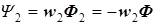

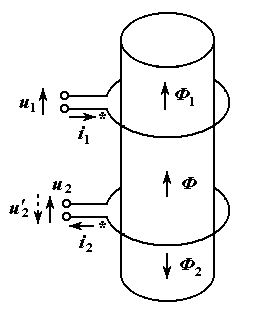
Рис. 5.16. Выбор однополярных зажимов и направлений магнитных потоков,

напряжений и токов на катушках трансформатора

По закону электромагнитной индукции

,

.

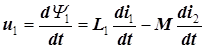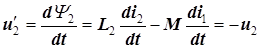Если эти соотношения записать в комплексной форме, то получатся уравнения (5.17) и (5.18).

Разделим почленно последнее равенство в формуле (5.17) на последнее равенство в (5.18):

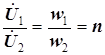, (5.19)

где 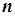- коэффициент трансформации трансформатора. Для трансформаторов, повышающих напряжение, 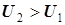, 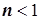; для понижающих трансформаторов , .

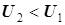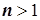По определению идеального трансформатора комплексная мощность, поступающая в первичную цепь, должна быть равна комплексной мощности, отдаваемой приемнику во вторичной цепи,

.

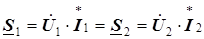Учитывая соотношения между напряжениями (5.19), получаем

,

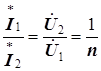следовательно,

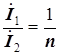. (5.20)

Уравнения (5.19) и (5.20) называются уравнениями идеального трансформатора.

И 5.11

Обычно уравнения идеального трансформатора записываются для действующих значений токов и напряжений , .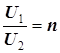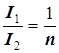

Векторная диаграмма токов и напряжений для идеального трансформатора показана на рис. 5.17. Построение диаграммы начинается с вектора магнитного потока 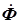. Токи, создающие магнитный поток, имеют те же фазы, что и поток. Напряжения на катушках трансформатора опережают их токи и магнитный поток на 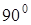по фазе в соответствии с уравнениями (5.17) и (5.18). Составляющие напряжени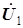й и 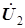(т.е. напряжения самоиндукции и взаимной индукции) на диаграмме не показаны, у идеального трансформатора они несоизмеримо больше по величине самих напряжени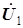й и .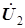

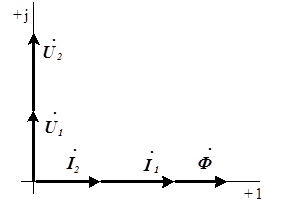
Рис. 5.17. Векторная диаграмма токов и напряжений идеального трансформатора ()

В автоматике и измерительной технике трансформаторы часто используются для преобразования сопротивлений. Комплексное сопротивление приемника, подключенного ко вторичной катушке трансформатора, равно по определению

.

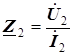Входное комплексное сопротивление трансформатора равно

.

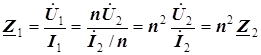И 5.12

Входное сопротивление трансформатора в 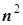раз больше сопротивления приемника, .

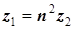Эта формула называется правилом трансформации сопротивлений. Реальные трансформаторы подчиняются этому правилу приблизительно.