И среднего линейного отклонения

Процент брака, % (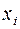)	Варианта (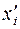)	Выполненный объем работ, тыс. деталей ()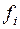
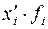
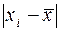
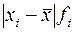
0,5–1,0	0,75			1,17
1,0–1,5	1,25			0,67
1,5–2,0	1,75			0,17
2,0–2,5	2,25			0,33
2,5–3,0	2,75			0,83
Итого	´			´

Для расчета среднего процента брака по предприятиям используем формулу средней взвешенной арифметической:

%.

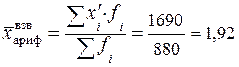Среднее линейное отклонение

%.

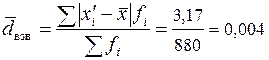Тогда процент брака отклоняется от средней от 0,17 до 1,17%, а в среднее линейное отклонение от средней арифметической составляет 0,004%.

Дисперсия – это средняя из квадратов отклонений от средней арифметической:

; ,

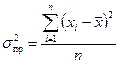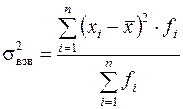где 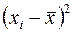– квадрат отклонения значения признака от средней арифметической.

Среднее квадратическое отклонение – показатель вариации, характеризующий величину, на которую в среднем признаки по единица наблюдения отличаются от средней арифметической:

; .

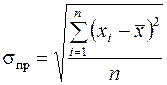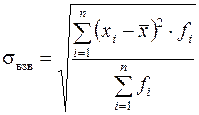Коэффициент вариации – это относительный показатель, исчисляемый как отношение среднего квадратического отклонения к средней арифметической:

.

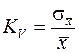Считается, что если коэффициент вариации достигает 33%, то совокупность нельзя признать качественно однородной.

Необходимость исчисления коэффициента вариации вызвана тем, что показатели вариации в абсолютных величинах, как правило, непосредственно несравнимы.

Пример. По данным приведенных в табл. 6.1. определить дисперсию, среднее квадратическое отклонение и коэффициент вариации.

Расчет показателей вариации приведен в табл. 6.3

Т а б л и ц а 6.3