Пример 1.1. Описать с помощью трех основных способов (перечислением элементов, заданием свойств элементов или порождающей функции) множество Х решений алгебраических уравнений:
а) x - 3 / x = 2;
б) cos 4 x = 1(0 ≤ x < 2 π);
в) | sin x | = 1.
→ а) x - 3 / x = 2 Û (x +1) (x- 3) = 0 Û x = -1 Ú x = 3 Þ
Þ X = {-1,3 }, Х = { x Î R | x - 3 / x = 2}.
→ б) cos 4 x = 1 (0 ≤ x < 2 π) Û x = kπ / 2 (k = 0,1,2,3) Þ
Þ X = {0, π / 2, π, 3/2 π }, X = { x Î [0, 2 π)| cos 4 x = 1 },
→ в) | sin x | = 1 Û sin x = ± 1 Þ X = { ± π / 2, ± 3 / 2 π, ± 5 / 2 π, … },
X = { x Î R | sin x = ± 1 }, X = { (2 n+ 1) π / 2 | nÎ Z }.
Пример 1.2. Показать эквивалентность (равномощность) следующих пар множеств X, Y:
а) X = [ 0, 1 ], Y = [ a, b ](a < b);
б) X = [-1, 1 ], Y = [ 0, 1 ];
в) X = (0,+ ∞), Y = (0, 1);
г) X = (-1, 1), Y = (- ∞,+ ∞).
→ В соответствии с определением эквивалентности (равномощности) множеств для решения сформулированной задачи достаточно найти (подобрать) функцию f: X ↔ Y, позволяющую установить взаимно однозначное соответствие между элементами множеств X и Y.
Для первых двух пунктов задачи, когда границы числовых множеств конечны, нахождение искомой функции, которая должна быть строго монотонной в своей области определения (множество Х для отображения f: X → Y или множество Y для отображения f: Y → X), не вызывает затруднений, так как в этом случае искомое отображение (функциональное преобразование) множеств X и Y фактически сводится к их деформации (масштабированию) и сдвигу начала (нижней границы).
Легко убедиться, что для первых двух заданных пар множеств в качестве таких функциональных преобразований можно использовать:
a) y = a + x (b-a) x, xÎ [ 0,1 ] Û x = (y-a) / (b-a); yÎ [ a,b ];
б) y = (x + 1) / 2, xÎ [-1, 1 ] Û x = 2 y - 1; yÎ [ 0, 1 ].
Несколько сложнее обстоит дело для третьего и четвертого пунктов задачи, так как среди границ множеств имеются как конечные, так и бесконечные. В этом случае график преобразующей функции должен иметь вертикальные или горизонтальные асимптоты.
Среди простейших элементарных функций такими свойствами обладают, например, дробно-рациональная, логарифмическая и некоторые тригонометрические (тангенс, арктангенс) функции. Несложно убедиться, что применительно к заданным парам множеств требуемые функциональные преобразования можно осуществить с помощью тригонометрических функций:
в) y = 2 / π arctg x, xÎ (0,+ ∞) Û x = tg (πy / 2), yÎ (0, 1);
г) y = tg (πx / 2), xÎ (-1, 1) Û x = 2 / π arctg y, yÎ (- ∞,+ ∞).
Пример 1.3. Найти сумму, произведение и разность множеств А, В:
а) A = { a,b,d }, B = { b,c,d,e,h };
б) A = [ 0, 3 ], B = (2, 6);
в) A, B – множества, составленные из элементов последовательностей
{ Xn } = { sin (nπ / 2) }, { Yn } = { cos (nπ / 2) }, (n є N);
г) A, B – множества, составленные из элементов последовательностей
{ Zn } = { n∙sin (nπ / 2) }, { Wn } = { n∙cos (nπ / 2) }, (n є N).
→ a) A + B = { a,b,c,d,e,h }, AB = { b,d }, A – В = { a }, B – A = { c,e,h }.
→ б) A + B = [ 0,6), AB = (2,3 ], A – В = [ 0,2 ], B – A = (3,6).
→ в) Легко заметить, что для элементов заданных последовательностей { Xn },{ Yn }справедливы равенства
Xn = 0, Yn = 1 при n = 4 k (k є N),
Xn = -1, Yn = 0при n = 4 k- 1 (k є N),
Xn = 0, Yn = -1при n = 4 k- 2 (k є N),
Xn = 1, Yn = 0 при n = 4 k- 3(k є N) Þ
Þ исходные множества состоят из одних и тех же элементов и равны A = B = { -1,0,1 } Þ
Þ A + B = AB = {-1,0,1}, A - B = B - A = Æ.
→ г) Так как по условиям задачи Zn = n ∙Xn, Wn = n ∙Yn, то равенства для элементов последовательностей { Zn }, { Wn } преобразуются к виду
Zn = 0, Wn = n при n = 4 k (k є N),
Zn = -n, Wn = 0при n = 4 k- 1 (k є N),
Zn = 0, Wn = -n при n = 4 k- 2 (k є N),
Zn = n, Wn = 0при n = 4 k- 3(k є N) Þ
Þ исходные последовательности и соответствующие множества можно описать следующим образом
{ Zn } = {1, 0, -3, 0, 5, 0,-7, 0, 9, 0,-11, 0, …},
A = {0, 1,-3, 5,-7, 9,-11, 13,-15, …},
{ Wn } = {0,-2, 0, 4, 0,-6, 0, 8, 0,-10, 0, 12, …},
B = {0,-2, 4,-6, 8,-10, 12,-14, …} Þ
Þ A + B = {0, 1,-2,-3, 4, 5,-6,-7, 8, 9,-10,-11, 12, 13,-14,-15, …}, AB = {0},
A – B = {1,-3, 5,-7, 9,-11, 13,-15 }, B - A = {-2, 4,-6, 8,-10, 12,-14, 16 }.
Пример 1.4. Исходя из определений теоретико-множественных операций, показать справедливость соотношений, характеризующих связи между различными операциями:
а) 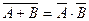 ,
, 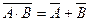 ;
;
б) 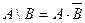 ,
, 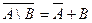 .
.
→ a) xÎ 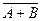 Û xÏ А+ В Û хÏ А Ù хÏ В Û хÎ Ā Ù хÎ
Û xÏ А+ В Û хÏ А Ù хÏ В Û хÎ Ā Ù хÎ 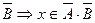 .
.
xÎ 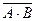 Û xÏ А∙В Û хÏ А Ú хÏ В Û хÎ Ā Ú хÎ
Û xÏ А∙В Û хÏ А Ú хÏ В Û хÎ Ā Ú хÎ 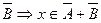 .
.
→ б) xÎ А \ В Û хÎ А Ù хÏ В Û хÎ A Ù хÎ 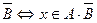 .
.
С учетом предыдущего равенства получаем
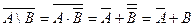 .
.
Пример 1.5. Представить в нормальной форме Кантора (разложить на конституенты) множество
D = 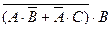 .
.
→ Руководствуясь сформулированными правилами разложения на конституенты (построения НКФ), последовательно получим:
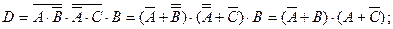
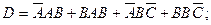
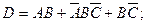
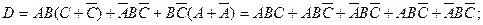
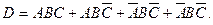
 2015-05-13
2015-05-13 1376
1376







