Мощность множества. Конечные и бесконечные множества

Мощность (кардинальное число) множества - такое свойство множества, которое остается после абстрагирования от качества (состава) его элементов (определение мощности по Кантору). Мощность множества А обозначается | А | или gard A.

Любые два множества А и В называются равномощными (эквивалентными), если между их элементами может быть установлено взаимно однозначное соответствие, т.е. существует взаимно однозначная функция f: A → B с областью определения А и множеством (областью) значений В. Таким образом, можно сказать, что мощность – это то общее, что есть у всех эквивалентных множеств. Понятие мощности введено Кантором для количественного сравнения различных множеств. С точки зрения правил сравнения (выявления общего), все множества делятся на конечные и бесконечные. В свою очередь бесконечные множества делятся на счетные и континуальные.

Конечное множество – множество, содержащее конечное число элементов; мощность n -элементного множества А равна числу его элементов, т.е. | А | = n; множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Æ; пустое множество является подмножеством любого множества и имеет нулевую мощность (| Æ | = 0). Из определения конечного множества следует – любые два конечные множества с одинаковым (равным) числом элементов эквивалентны (между ними легко установить взаимно однозначное соответствие – для этого достаточно, например, ввести нумерацию элементов).

Одна из особенностей конечного множества заключается в том, что его всегда можно задать путем перечисления элементов. Ясно, что это не всегда удобно (когда число элементов велико), но довольно часто другие способы просто неприемлемы. Последнее относится, например, к ситуации, когда нужно описать подмножество студентов, объединенных в определенную группу (поток). Очевидно, в этом случае придумать какое-то свойство или порождающую функцию, позволяющие однозначно выделить группу студентов из всего множества студентов вуза (факультета), практически невозможно (да в этом и нет необходимости – достаточно составить список студентов).

Бесконечное множество - всякое множество А, имеющееправильную часть В, равномощную всему (целому) множеству А, т. е. В Ì А и |В| = |А|. Так, например, множество М квадратов натуральных чисел является правильной частью всего множества N натуральных чисел (взаимно однозначное соответствие между этими множествами очевидно); следовательно, оба эти множества обладают одинаковой мощностью и подпадают под определение бесконечных множеств. В то же время это определение не подходит к конечным множествам, так как мощность (число элементов) правильной части любого конечного множества всегда меньше мощности полного множества.

Счетное множество - любое бесконечное множество, равномощное множеству N натуральных чисел. Мощность счетного множества принято обозначать 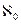(алеф - нуль). Отличительная особенность счетного множества – все его элементы могут быть пронумерованы. И хотя любое конечное множество также обладает этой особенностью, оно, по определению, к счетным множествам не относится. Примеры часто встречающихся счетных множеств: любые бесконечные подмножества множества N натуральных чисел; множества целых и рациональных чисел и их бесконечные подмножества (одним из таких подмножеств является, в частности, множество N);

множества, составленные из элементов бесконечных числовых последовательностей как функций натурального аргумента (если эти множества после исключения одинаковых элементов не трансформируются в конечные).

Замечание. С возможностью нумерации элементов счетного множества связан тот факт, что довольно часто такого рода множества описываются посредством перечисления элементов. Это характерно, например, при задании (описании) бесконечных числовых последовательностей и рядов, когда по записанным нескольким первым членам последовательности (ряда) видна закономерность их изменения и, как следствие, запись последующих членов с помощью выявленной закономерности не вызывает затруднений. Простейшей иллюстрацией к вышесказанному могут служить применяемые на практике описания множеств натуральных и целых чисел, а именно:

N = { 1, 2, 3, 4,…}; Z = { 0, ±1, ±2, ±3,…}; Z= {…-3,-2,-1, 0, 1, 2, 3,…}.

Континуальное множество - любое бесконечное множество, равномощное множеству R действительных чисел. Говорят, что всякое континуальное множество имеет мощность континуума. Такой мощностью обладают, например:

множество всех подмножеств всякого счетного множества;

множество точек, принадлежащих некоторой прямой или поверхности;

множество всех действительных чисел некоторого интервала (a,b) или отрезка [ a,b ] (см. пример1.2).

В отличие от счетного множества,элементы континуального множества не могут быть пронумерованы, т.е. множество-континуум несчетно. Справедливость данного утверждения подтверждается теоремой Кантора, одно из доказательств которой представлено ниже.

Теорема Кантора. Множество действительных чисел отрезка [0,1] несчетно.

→ Докажем теорему методом от противного. Для этого предположим, что множество счетно, т.е. может быть пронумеровано. Расположим все числа, изображенные бесконечными десятичными дробями, в порядке их нумерации:

Рассмотрим любую бесконечную дробь 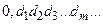, у которой 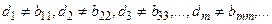. Эта дробь не может войти в указанную последовательность, так как от первого числа она отличается первой цифрой, от второго - второй цифрой и т.д.

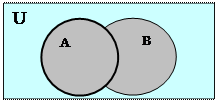
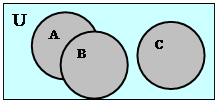
Геометрическая интерпретация множеств. Для геометрического (графического) изображения множеств и их свойств (связей между ними) довольно часто используются так называемые диаграммы Эйлера-Венна, представляющие собой в общем случае некоторый прямоугольник на плоскости и вложенные в него круги.

Так, если в рамках конкретно решаемой задачи рассматривается некая система S = { A,B,C,…,G }частных множеств, то кругами (круги Эйлера), находящимися внутри прямоугольника, изображаются любые множества из S, а прямоугольником - некоторое фиксированное универсальное множество (множество-универсум) U, включающее в себя в качестве подмножеств всю систему S частных множеств, т.е.

" МÎ S: M Ì U. При этом каждое множество мыслится как множество точек, принадлежащих изображающему его кругу Эйлера.

Замечание. Ясно, что множество-универсум U должно быть либо задано, либо очевидно из контекста задачи. Так, для S = { A, B, С }, где

A = { a,b,c }, B = { b,с,d,e }, C = { f, g },

в качестве универсального множества можно использовать как весь латинский алфавит, так и множество U = { a,b,c,d,e,f,g }. Круги, иллюстрирующие множества А и В на рисунке, пересекаются, так как эти множества имеют общие элементы.

Геометрическая иллюстрация множеств