Свойства дисперсии. D1). , тогда и только тогда, когда п.н

D1). 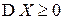, 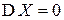тогда и только тогда, когда 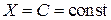п.н.

▲ Поскольку 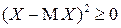для любог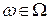о , то 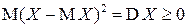в соответствии со свойством М4) математического ожидания

Предположим, что 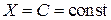п.н. Тогда 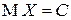и 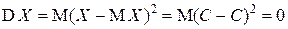. Обратно, если 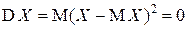, то в соответствии со свойством М4) математического ожидания 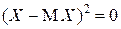п.н., а значит 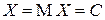п.н. ■.

D2). Дисперсия не изменяется при прибавлении к случайной величине константы:

▲ ■.

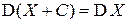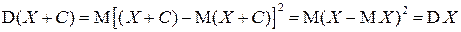D3). Константа из-под знака дисперсии выносится с квадратом:

▲ ■.

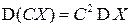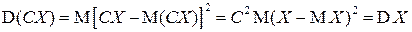Дисперсия имеет размерность квадрата случайной величины. Характеристикой рассеивания, размерность которой совпадает с размерность случайной величины, является среднее квадратическое отклонение 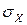(стандартное отклонение), определяемое как корень арифметический из дисперсии:

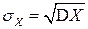Поэтому часто пишут: .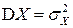

Другие используемые на практике числовые характеристики положения.

Величина 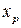, определяемая равенством 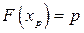, называется
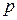- квантилем распределения случайной величины .

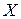Квантиль называется медианой распределения случайной величины 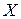. Другими словами, медиана – это значение на числовой прямой, для которого

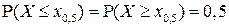
Модой распределения непрерывной случайной величины 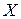называется число 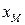, при котором плотность вероятностей 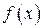достигает максимального значения. Распределения с одной модой называются унимодальными, а распределения с несколькими модами – мультимодальными.