Пусть 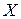 - некоторая случайная величина, определенная на вероятностном пространстве
- некоторая случайная величина, определенная на вероятностном пространстве 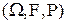 , закон распределения которой известен (дискретный или непрерывный);
, закон распределения которой известен (дискретный или непрерывный); 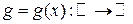 - неслучайная функция;
- неслучайная функция; 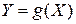 - функция от случайной величины
- функция от случайной величины 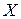 .
.
Везде далее мы будем предполагать, что преобразующая функция  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1. Область определения 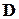 функции
функции  содержит множество
содержит множество 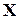 возможных значений случайной величины
возможных значений случайной величины 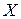 :
: 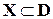 ;
;
2. Функция  является борелевской, то есть измеримой относительно борелевской
является борелевской, то есть измеримой относительно борелевской 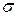 -алгебры
-алгебры 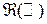 . Это означает, что для любого борелевского множества
. Это означает, что для любого борелевского множества 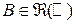 его образ
его образ 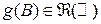 .
.
Первое условие обеспечивает корректность функционального преобразования 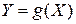 . Второе условие гарантирует, что функция
. Второе условие гарантирует, что функция 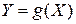 от случайной величины
от случайной величины 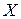 также будет случайной величиной. Действительно, если функция
также будет случайной величиной. Действительно, если функция  является борелевской, то по определению случайной величины
является борелевской, то по определению случайной величины 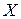 для любого борелевского множества
для любого борелевского множества 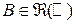 множество
множество 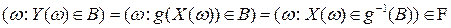 , поскольку полный прообраз
, поскольку полный прообраз 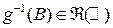 ).
).
Замечание. Класс борелевских функций на числовой прямой очень широк и покрывает все потребности практики (в частности, ему принадлежат все ограниченные кусочно-непрерывные функции). Поэтому требование того, что функция  должна быть борелевской, для приложений ограничительным не является.
должна быть борелевской, для приложений ограничительным не является.
Задача состоит в нахождении математического ожидания 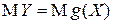 . Существует два способа решения этой задачи:
. Существует два способа решения этой задачи:
а) По закону распределения случайной величины 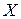 находится закон распределения случайной величины
находится закон распределения случайной величины 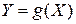 и используются стандартные формулы (2.7) и (2.8);
и используются стандартные формулы (2.7) и (2.8);
б) Математическое ожидание 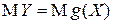 находится с помощью основной теоремы о математическом ожидании.
находится с помощью основной теоремы о математическом ожидании.
Теорема (основная теорема о математическом ожидании или теорема о замене переменных).
Пусть 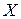 - некоторая случайная величина, закон распределения которой известен, случайная величина
- некоторая случайная величина, закон распределения которой известен, случайная величина 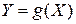 является функцией от случайной величины
является функцией от случайной величины 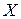 .
.
1. Если случайная величина 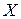 является дискретной, принимающей значения
является дискретной, принимающей значения 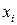 с вероятностями
с вероятностями 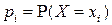 ,
, 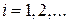 , и при этом ряд
, и при этом ряд 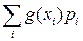 абсолютно сходится (
абсолютно сходится (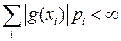 ), то у случайной величины
), то у случайной величины 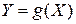 существует математическое ожидание и
существует математическое ожидание и
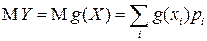 .
.
2. Если случайная величина 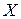 является непрерывной с плотностью вероятностей
является непрерывной с плотностью вероятностей 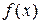 и интеграл
и интеграл 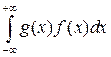 абсолютно сходится (
абсолютно сходится (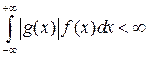 ), то у случайной величины
), то у случайной величины 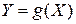 существует математическое ожидание и
существует математическое ожидание и
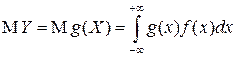 .
.
(без доказательства).
Смысл основной теоремы о математическом ожидании: Для нахождения математического ожидания случайной величины 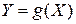 , являющейся функцией от случайной величины
, являющейся функцией от случайной величины 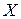 , не требуется знать закон распределения случайной величины
, не требуется знать закон распределения случайной величины 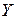 , достаточно лишь знать закон распределения случайной величины
, достаточно лишь знать закон распределения случайной величины 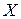 .
.
 2015-05-13
2015-05-13 2735
2735