ГЛАВА I. ТЕОРИЯ ОПРЕДЕЛИТЕЛЕЙ
Считаем известным определение бинарного отношения, отображения, кортежа длины n. Напомним, что отображение j: А®В называется сюръективным, если
" bÎB $aÎA (j(a)=b).
Отображение j: А®В называется взаимно однозначным или инъективным, если
" а1, а2ÎА (а1¹ а2 Þ j(а)¹j(а2)).
И наконец, отображение j: А®В называется биекцией, если оно одновременно сюръективно и инъективно. Отображение множества М в себя называется преобразованием множества М.
Определение. Любой упорядоченный кортеж длины n называется перестановкой из n элементов.
Теорема. Число всех перестановок из n элементов равно n!.
Доказательство
При доказательстве будем использовать метод математической индукции по числу элементов.
1. При n=1 теорема верна, что очевидно.
2. Предположим, что теорема верна для n и подсчитаем число различных перестановок из n+1 элемента. Из n элементов, по индуктивному предположению, можно составить n! перестановок, добавить к каждой из них 1 элемент можно (n+1) способами, тогда всего различных перестановок будет n!(n+1)=1´2´...´n´(n+1)=(n+1)!. Теорема доказана.
Перестановку можно также определить как строго линейно упорядоченное множество.
Примеры: Из элементов множества {1,2,3,4,5} можно составить 5!=120 различных перестановок. Например, J1=(1,2,3,4,5); J2=(1,2,4,3,5)...
В общем виде перестановки принято записывать
J=(I1, I2 ,..., Ik).
Определение. Если в перестановке J символы Iк и Iв таковы, что Iк > Iв, но Iк предшествует Iв, то говорят, что символы Iк и Iв образуют инверсию.
Пример: В перестановке J=(3,2,1,4,5) символы 3 и 2, 3 и 1, 2 и 1 образуют инверсию.
Определение. Если в перестановке J число инверсий четно, то такая перестановка называется четной, если число инверсий нечетно, то перестановка называется нечетной.
Определение. Если в перестановке J поменять местами два символа, то такое преобразование перестановкиназывается транспозицией.
Теорема. Всякая транспозиция меняет четность перестановки.
Доказательство
Для доказательства рассмотрим случай, когда транспонируемые символы стоят рядом. Пусть
J1=(I1, I2,..., Ik-1, I, J, Ik+2,..., In).
В результате транспозиции получим перестановку:
J2=(I1, I2,..., Ik-1, J, I, Ik+2,..., In).
Очевидно, для любого элемента Is верно следующее: если J и Is составляли инверсию в J1, они составляют инверсию и в J2, аналогично, если Is и I составляли инверсию в J1, то они составляют инверсию и в J2, так как их взаимное расположение не изменилось. Таким образом, общее число инверсий, которые образуют символы I и J с остальными символами, одинаково для J1 и J2, а сами символы I и J, если они образовывали инверсию в J1, то не образуют инверсии в J2 и наоборот. То есть в любом случае число инверсий в перестановках J1 и J2 отличается на 1, следовательно, эти перестановки имеют разную четность.
Теперь пусть между транспонируемыми элементами I и J находится некоторое количество символов
J1=(I1, I2,..., Ik-1, I, e1, e2,..., em, J,..., In),
J2=(I1, I2,..., Ik-1, J, e1, e2,..., em, I,..., In).
чтобы поменять местами элементы I и J, сначала элемент I будем менять местами последовательно с элементами e1, e2,..., em, J, для этого нам придется сделать m+1 транспозицию, а затем элемент J будем менять местами с элементами em, еm-1,..., e2, e1, то есть совершим еще m транспозиций. Таким образом, чтобы поменять местами элементы I и J, нам пришлось сделать m+1+m=2m+1 транспозицию, а так как каждая следующая транспозиция меняет четность перестановки, то 2m+1 транспозиция изменит четность перестановки J1.
Теорема. Все n! перестановок из n элементов можно расположить так, что каждая следующая перестановка будет получаться из предыдущей путем одной транспозиции, начинать можно с любой перестановки.
Следствие. Для n³2 число четных перестановок равно числу нечетных перестановок и равно 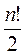
 2015-05-13
2015-05-13 2751
2751