Перестановки и подстановки

Определение 3.1: Пусть 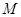– конечное множество, состоящее из различных элементов. Расположение этих элементов в определенном порядке называется перестановкой.

Теорема 3.1: Количество различных перестановок из элементов равно .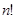

Определение 3.2: Транспозицией называется такое преобразование перестановки, при котором меняются местами какие-либо два элемента перестановки, а остальные остаются на месте.

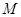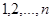Элементы множества могут быть перенумерованы при помощи натуральных чисел , и так как в интересующих нас вопросах природа элементов множества 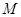нас не интересует, то мы примем, что элементами множества 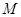служат сами эти числа .

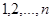Теорема 3.2: Все 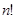перестановок из элементов можно расположить в таком порядке, что каждая следующая будет получаться из предыдущей одной транспозицией, причем начинать можно с любой перестановки.

Следствие: От любой перестановки можно перейти к любой другой перестановке при помощи конечного числа транспозиций.

Определение 3.3: Говорят, что в данной перестановке из первых натуральных чисел числа 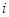и 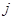образуют инверсию, если 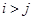, но 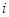стоит в этой перестановке раньше .

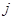Определение 3.4: Перестановка называется четной, если ее числа составляют четное число инверсий, и нечетной – в противном случае.

Теорема 3.3: Всякая транспозиция меняет четность перестановки.

Теорема 3.4: Число четных перестановок равно числу нечетных перестановок из символов и равно .

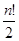Определение 3.5: Взаимно-однозначное отображение конечного множества 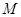на себя называется подстановкой.

Очевидно, что две перестановки, записанные одна под другой, задают подстановку.

Например: .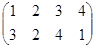

Определение 3.6: Подстановка, определяемая двумя перестанов-ками, называется четной, если четности перестановок совпадают, и нечетной – в противном случае.