Группа подстановок

Рассмотрим множество подстановок из n элементов

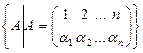S_n=

и введем на этом множестве операцию умножения. Произведением подстановок А и В будем называть результат последовательного выполнения подстановок А и В (слева направо).

Примеры

1. Найти произведение подстановок А и В если

, ,

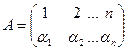тогда

.

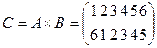2. Найти произведение подстановок А и В если

, ,

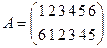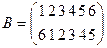тогда

.

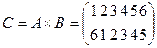Теорема. Алгебра (S_n, *) - группа.

Доказательство

Проверим выполнимость всех аксиом группы. Аксиома замкнутости выполняется по определению бинарной алгебраической операции * на множестве S_n. Проверим аксиому ассоциативности. Пусть

; ; .

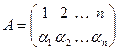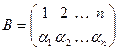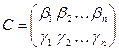Найдем образ произвольного элемента i при выполнении подстановки (A*B) *C. i®a_i ®b_i ®g_i, то есть образом элемента i будет элемент g_i. Теперь найдем образ того же элемента при выполнении подстановки A*(B*C): a_i ®b_i ®g_i ®a_i ®g_i и a_i ® i ®g_i . Так как элемент i выбран произвольно, то любой элемент верхней строки подстановки А отображается в один и тот же элемент нижней строки подстановки С, независимо от последовательности выполнения подстановок. Легко видеть, что роль единицы играет тождественная подстановка

E=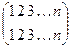

и, наконец, для любой подстановки A= 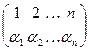существует подстановка

A^-1= 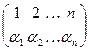, такая, что A*A^-1=E; A^-1* A =E, таким образом, все аксиомы группы выполняются. Теорема доказана.

Замечание. Умножение подстановок не коммутативно. Приведем пример.

A*B=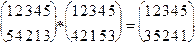

B*A= ,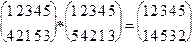

то есть A*B ¹B*A.