N-мерное арифметическое пространство

Определение. Два вектора a и b=(b₁,b₂,...,b_n) будут считаться равными, если a_i=b_i " i =1,2,...,n

Примеры: 1) множество векторов плоскости, пространства;

2) коэффициенты линейного уравнения с n неизвестными составляют n-мерный вектор;

3) любое решение системы линейных уравнений с n неизвестными будет n-мерным вектором;

4) в матрице размера n´n любая строка и любой столбец являются n- мерными векторами.

Определение. Суммой векторов a и b называется вектор

a+b=(a₁+b₁,a₂+b₂,...,a_n+b_n).

Роль нуля играет вектор 0=(0,0,...,0).

Определение. Вектор -a= (-a₁,-a₂,...,-a_n) называется противоположным вектору a.

Определение. Произведением вектора a на число k называется вектор ka=ak= (ka₁,ka₂,...,ka_n).

Свойства умножения вектора на число

Свойство 1. "a,b "kÎR (k(a±b)=ka±kb)

Свойство 2. "a " k,l ÎR ((k ± l)a= k a± l a

Свойство 3. "a " k,l ÎR (k(l a)=(kl) a)

Свойство 4. "a (1×a=a)

Доказать самостоятельно.

Следствие 1. "a (0×a=0)

Следствие 2. " kÎR (k×0=0)

Следствие 3. "a ((-1)×a=-a)

Доказать самостоятельно.

Определение. Множество всех n-мерных векторов с действительными координатами с операциями сложения и умножения вектора на число называется n-мерным векторным пространством.

Определение. Вектор b из n-мерного пространства называется пропорциональным вектору a, если существует такое число k, что b= ka.

(Нулевой вектор пропорционален любому вектору.)

Обобщением понятия пропорциональности векторов является понятие линейной комбинации векторов.

Определение. Вектор b из n-мерного пространства называется линейной комбинацией векторов a₁,a₂,...,a_s, если существуют такие числа t₁,t₂,...,t_s, что b= t₁a₁+ t₂ a₂+...+t_s a_s. (1)

Определение. Система векторов a₁,a₂,...,a_r (r³2) называется линейно зависимой, если хотя бы один из этих векторов является линейной комбинацией остальных, и линейно независимой в противном случае.

Можно определить иначе. Система векторов a₁,a₂,...,a_r (r³2) называется линейно зависимой, если существуют такие числа t₁,t₂,...,t_r, хотя бы одно из которых отлично от 0, что имеет место равенство t₁a₁+ t₂ a₂+...+t_r a_r=0

Система векторов a₁,a₂,...,a_r называется линейно независимой, если такое равенство возможно лишь при всех t_i равных 0.

Свойство. Если некоторая подсистема системы векторов a₁,a₂,...,a_s линейно зависима, то и вся система линейно зависима.

Доказательство

Пусть дана система векторов а_i1.a_i2,...,а_s, и подсистема этой системы векторов а_i1.a_i2,...,а_ir, где r<s, линейно зависима, то есть $ t_i1, t_i2,..., t_ir, не все равные 0, такие, что t_i1 а_i1 + t_i2a_i2+...+t_ira_ir, отсюда получаем t₁₁a₁₁+t₂₂a₂₂+...+t_i2a_i2+...+t_ira_ir+...+t_sa_s=0 и не все t_i= 0, следовательно, система векторов a₁,a₂,...,a_s линейно зависима.

Следствие 1. Система векторов, содержащая два равных вектора, линейно зависима.

Следствие 2. Система векторов, содержащая два противоположных вектора, линейно зависима.

Следствие 3. Система векторов, содержащая нулевой вектор, линейно зависима.

Следствие 4. Если система векторов линейно независима, то и всякая ее подсистема линейно независима.

Определение. Линейно независимую систему n-мерных векторов a₁,a₂,...,a_s назовем максимальной линейно независимой системой, если добавление к этой системе любого n-мерного вектора b делает эту систему линейно зависимой.

Возникает вопрос: какое максимальное число векторов может составлять линейно независимую систему. Рассмотрим векторы

е₁=(1,0,0,...,0),

………………(2)

е_n=(0,0,0,...,1).

Эти векторы называются единичными векторами n-мерного пространства.

Предложение. Система единичных векторов (2) линейно независима.

Доказательство. Рассмотрим равенство

k₁e₁+k₂e₂+...+k_ne_n=0,

k₁(1,0,0,...,0)+ k₂(0,1,0,...,0)+ k_n(0,0,0,...,1)=1,

(k₁, 0,..., 0)+(0, k₂,0,..., 0)+...+(0, 0, 0,..., k_n)=0,

(k₁, k₂,..., k_n)=0, то есть k_i=0 "_i=1,..., n.

Таким образом, мы получили, что система единичных векторов (2) линейно независима.

Предложение. Любой вектор n-мерного пространства можно представить как линейную комбинацию векторов системы (2).

Доказательство - самостоятельно.

Определение. Будем говорить, что вектор b линейно выражается через систему векторов а₁ , а₂,..., а_r, если b является линейной комбинацией векторов, входящих в систему а₁, а₂,..., а_r.

Определение. Система векторов b₁, b₂,..., b_s линейно выражается через систему векторов а₁, а₂,..., а_r , если всякий вектор b _i является линейной комбинацией векторов системы a (" i =1,2,...,s).

Лемма. Если система векторов a линейно выражается через систему векторов b, а система векторов b линейно выражается через систему векторов g, то система векторов a линейно выражается через систему векторов g.

Доказательство

Пусть даны системы векторов

а₁, а₂,..., а_r; b₁, b₂,..., b_s; g₁, g₂,..., g_t.

По условию, система векторов a линейно выражается через систему векторов b, а система векторов b линейно выражается через систему векторов g, то есть

;

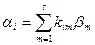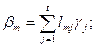
тогда

,

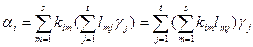то есть любой вектор системы a линейно выражается через систему векторов g.

Теорема. Если в n-мерном векторном пространстве даны две системы векторов а₁, а₂,..., а_r иb₁, b₂,..., b_s и все векторы системы a линейно выражаются через векторы системы b, тогда если r>s, то система векторов a линейно зависима.

Доказательство

Докажем методом математической индукции по числу s.

1. s=1, тогда а₁ =с₁ b₁, а₂ =с ₂b₁,..., а_r =с_r b₁.

Если с₁=0, то система векторов a линейно зависима, так как содержит нулевой вектор а₁.

Если с₁¹0, то имеем линейную зависимость (- с ₂) а₁ + с₁ а₂+0 а₃+...+0 а_r=0, следовательно, система a линейно зависима.

2. Предположим, что утверждение верно для s-1 вектора, и докажем для s. Пусть

a₁=с₁₁b₁+с₁₂b₂+...+c_1sb_s

a₂=c₂₁b₁+c₂₂b₂+...+c_2sb_s

...................................

a_r=c_r1b₁+c_r2b₂+...+c_rsb_s.

Если с₁₁= c₂₁=...= c_r1=0, то утверждение справедливо, так как система векторов a в этом случае линейно выражается через s-1 вектор b₂,..., b_s.

Пусть один из коэффициентов отличен от нуля. Не нарушая общности доказательства, можем считать, что с₁₁ ¹0. Рассмотрим векторы

................................................. (*)

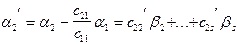
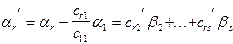
вновь построенные r-1 вектор, линейно выражаются через s-1 вектор, тогда, в силу индуктивного предположения, векторы 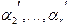линейно зависимы, то есть $b₂, b₃,...,b_rÎR, среди которых есть отличные от нуля, такие что 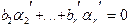. Подставив это в равенство (*), получим

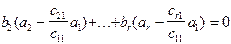
или после преобразования

.

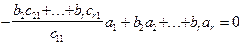Теорема доказана.

Определение. Две системы векторов называются эквивалентными, если каждая из них линейно выражается через другую.

Следствие 1. Всякие две эквивалентные линейно независимые системы векторов содержат равное число векторов.

Следствие 2. Всякие s векторов n-мерного пространства составляют при s>n линейно зависимую систему.

Доказательство. Рассмотрим систему s векторов n-мерного пространства (s>n) a₁=(a₁₁, a₁₂,..., a_1n),

a₂=(a₂₁, a₂₂,..., a_2n),

............................ (3)

a_s=(a_s1, a_s2,..., a_sn).

По утверждению, эта система линейно выражается через систему (2), следовательно, по доказанной теореме она линейно зависима.

Следствие 3. Всякая максимальная линейно независимая система векторов n-мерного пространства состоит из n векторов.

Следствие 4. Если в данной линейно зависимой системе векторов взяты две в ней максимально линейно независимые подсистемы, то эти подсистемы содержат равное число векторов.