Пусть дана система n линейных уравнений с n неизвестными, причем определитель системы отличен от 0.
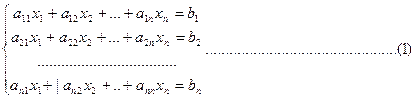
Перепишем эту систему в матричной форме, если
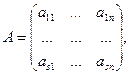
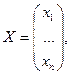
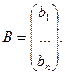
тогда систему (1) можно записать в матричном виде, то есть
AX=B (2)
Так как матрица А невырожденная, тогда для нее существует обратная. Умножив обе части уравнения (2) на А-1, получим
A-1(AX)=A-1BÞ (A-1A)C=A-1B Þ C=A-1B (3)
Покажем, что Х - решение уравнения (2)
A(A-1B)= (AA-1)B=ЕВ=В Û B=B
Так как для любой невырожденной матрицы существует единственная обратная, то решение системы уравнений (1), записанной в матричной форме (2), однозначно определяется формулой (3). Любой элемент матрицы столбца, стоящей в правой части формулы (3), имеет вид
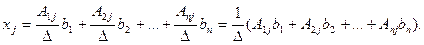
Получим формулы Крамера в общем виде, где
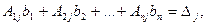
то есть определитель, полученный из D заменой j столбца столбцом свободных членов.
Пример. Решить систему уравнений
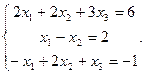
Запишем в матричном виде AX=B, где
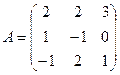 ;
; 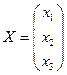 ;
; 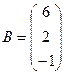
Найдем определитель матрицы А
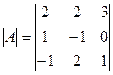 =-1;
=-1; 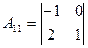 =-1;
=-1; 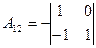 =-1;
=-1; 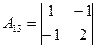 =1;
=1;
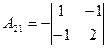 =4;
=4; 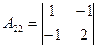 =5;
=5; 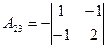 =-6;
=-6; 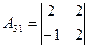 =3;
=3;
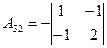 =3;
=3; 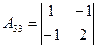 =-4;
=-4;
А= 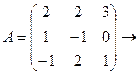
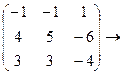
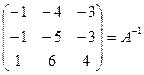
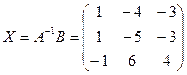
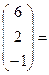
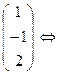 Х1=1; Х2=-1; Х3=2
Х1=1; Х2=-1; Х3=2
Решим ту же систему по формуле Крамера. D=-1
|
|
|
D1= 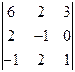 =-1; D2 =
=-1; D2 = 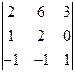 =1; D3=
=1; D3= 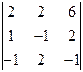 =-2
=-2
x 1= 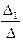 =1; x 2=
=1; x 2= 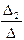 =-1; x 3=
=-1; x 3= 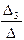 =2.
=2.
Упражнения
1. Вычислить определители:
a) 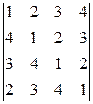 ;
;
b) 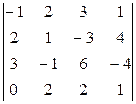 ;
;
c) 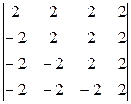 ;
;
d) 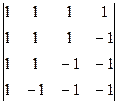 .
.
2. Решить матричные уравнения
a) 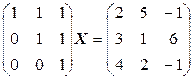 ;
;
b) 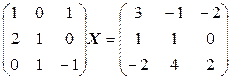 ;
;
c) 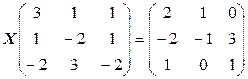 ;
;
d) 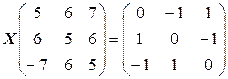 ;
;
e) 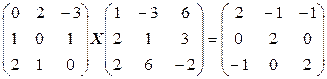
3. Решить системы уравнений по формулам Крамера
a) 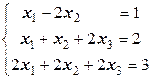 ; b)
; b) 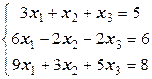
 2015-05-13
2015-05-13 799
799








