Параллельное соединение. Активная, реактивная и полная проводимости. Треугольники проводимостей и токов

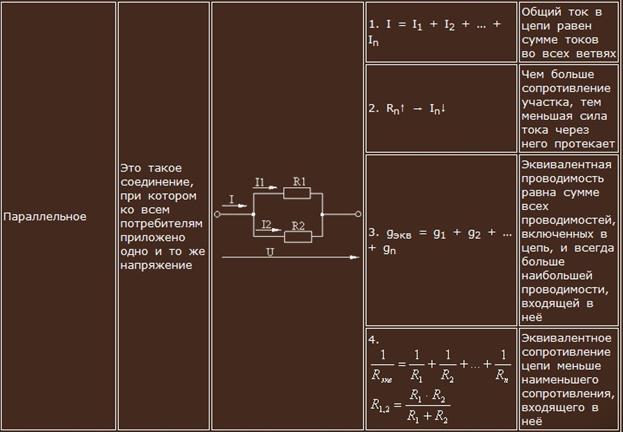
Активные составляющие токов равны

I_1а = I₁ cos φ₁, I_2а = I₂ cos φ₂,

I_а = I_1а + I_2а.

Реактивные составляющие токов равны

I_1р = I₁ sin φ₁, I_2р = I₂ sin φ₂,

I_р = I_1р - I_2р.

В последнем уравнении взят знак минус, поскольку составляющие I_1р (индуктивная) и I_2р (емкостная) направлены в разные стороны от оси U.

Полный ток находится из уравнений

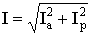, φ = arctg(I_р / I_а).

Представим комплексную проводимость в алгебраической форме

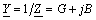. (2.10.5)

Действительную часть комплексной проводимости G называют активной проводимостью, а мнимую В — реактивной. На рис. 2.10.2, а сделаны построения, соответствующие комплексному выражению (2.10.5).

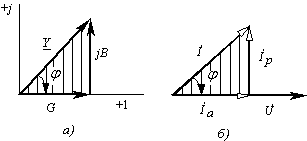
Рис. 2.10.2. Треугольники проводимостей и токов

Заштрихованный прямоугольный треугольник на рис. 2.10.2, а называют треугольником проводимостей. Из треугольника очевидны соотношения.

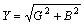; G = Y cos j; В = Y sin j;

tg j = B / G; cos j = G / Y; sin j = B / Y. (2.10.6)

Выразим активную и реактивную составляющие проводимости ветви через ее активное и реактивное сопротивления.

Рассмотрим, например, проводимость ветви с элементами R ₁ и jX_L

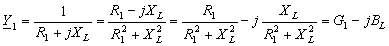. (2.10.7)

При получении соотношения (2.10.7) числитель и знаменатель домножены на сопряженный комплекс .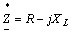

Следует обратить внимание на то, что мнимая часть комплексной проводимости ветви с индуктивным элементом отрицательная. Если бы подобным образом было получено соотношение для второй ветви, содержащей емкостный элемент, то формулы имели бы тот же вид, но мнимая часть была бы положительной.

Итак,

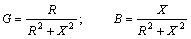
или

G = R / Z ²; B = X / Z ². (2.10.8)

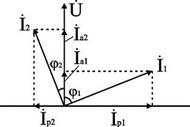
Построение треугольника тока очевидно из рис. 2.10.2, б. На векторной диаграмме рис. 2.10.2, б вектор тока спроецирован на направление вектора напряжения. Полученный при этом треугольник называют треугольником тока. Катеты прямоугольного треугольника тока называют активной и реактивной составляющими: активная составляющая тока I _a параллельна напряжению, а реактивная I _р — ортогональна.

Из треугольника тока можно получить следующие выражения:

I _a = I cosj, I _р = I sinj. (2.10.9 а)

Так как I = UY, cosj = G / Y, sinj = В / Y, получаем, после подстановки в (2.10.9 а),

I _а = GU и I _р = BU. (2.10.9 b)