Резонанс Токов

Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. Резонанс токов может возникнуть в параллельной цепи (см. рис. 2.17, а), одна из ветвей которой содержит L и r, а другая С и r.

Резонансом токов называется такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность. На рис. 2.17, г изображена векторная диаграмма цепи рис. 2.17, а при резонансе токов.

Как видно из векторной диаграммы, общий ток цепи совпадает по фазе с напряжением, если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю:

I _1р = I _2р.

Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю:

I _1р - I _2р = 0.

Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей:

I _а = I _1а + I _2а.

Выразив реактивные токи через напряжения и реактивные проводимости, получим

Ub_L = Ub_С,

откуда

b_L = b_С.

Итак, при резонансе токов реактивная проводимость ветви с индуктивностью равна реактивной проводимости ветви с емкостью.

Выразив b_L и b_С через сопротивления соответствующей ветви, можно определить резонансную частоту контура:

xL	=	xC	=	2π fL	=	1 2π fC	,
r 12+ xL 2	x 22 + xC 2	r 12 + (2π fL)2	r 22+ (   )2 2π fC

откуда

f рез =		√	L/C - r 12	.
2π√ LC	L/C - r 22

В идеальном случае, когда r ₁ = r ₂ = 0,

f рез =		.
2π√ LC

При резонансе токов коэффициент мощности равен единице:

cos φ = 1.

Полная мощность равна активной мощности:

S = P.

Реактивная мощность равна нулю:

Q = Q_L - Q_C = 0.

Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений, которые были подробно рассмотрены в § 2.12.

Реактивная энергия действует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактивной энергией между потребителями цепи и источником питания не происходит. Ток в проводах, соединяющих цепь с источником, обусловлен только активной мощностью.

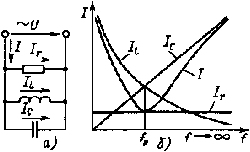Рис. 2.19. Электрическая цепь (а) и графики зависимости Ir, IL, IC и I от частоты f (б)

Для резонанса токов характерно, что общий ток при определенном сочетании параметров цепи может быть значительно меньше токов в каждой ветви. Например, в идеальной цепи, когда r ₁ = r ₂ = 0 (см. рис. 2.18, а), общий ток равен нулю, а токи ветвей с емкостью и индуктивностью существуют, они равны по модулю и сдвинуты по фазе на 180°. Резонанс в цепи при параллельном соединении потребителей называется резонансом токов.

Резонанс токов может быть получен путем подбора параметров цепи при заданной частоте источника питания или путем подбора частоты источника питания при заданных параметpax цепи.

Представляет интерес влияние частоты источника питания на значения токов в цепи, например в цепи, изображенной на рис. 2.19, а.

Ток в ветви с индуктивностью обратно пропорционален частоте:

I_L = U/ 2π fL,

а ток в ветви с емкостью прямо пропорционален частоте:

I_С =U 2π fC.

Ток в ветви с активным сопротивлением не зависит от частоты ¹:

I_r = U/r.

Вектор общего тока в цепи равен геометрической сумме векторов токов ветвей: Ī =Ī_r + Ī_L+Ī_С,